题目内容
12.在正方体的八个顶点中,有四个恰好是正四面体(四个面都是正三角形的三棱锥)的顶点,则正方体的表面积与此正四面体的表面积的比值为( )| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | $\frac{{\sqrt{6}}}{2}$ | D. | $\frac{{\sqrt{3}}}{3}$ |
分析 由题意可得该正四面体恰好以正方体的面对角线为棱,设出正方体棱长,从而求出正四面体棱长,由此能出结果.
解答 解:由题意可知该正四面体恰好以正方体的面对角线为棱,
故设正方体的棱长为a,则正四面体的棱长为$\sqrt{2}$a,
正方体的表面积为6a2,正四面体的表面积为4×$\frac{1}{2}×\sqrt{2}a×\sqrt{2}a×sin60°$=2$\sqrt{3}a$2,
正方体的表面积与此正四面体的表面积的比值为:$\frac{6{a}^{2}}{2\sqrt{3}{a}^{2}}$=$\sqrt{3}$.
故选:B.
点评 本题考查棱柱、棱锥、棱台的表面积公式,得到正四面体恰好以正方体的面对角线为棱是解决问题的关键,属基础题.

练习册系列答案
相关题目
5.某校高三毕业汇演,要将A、B、C、D、E、F这六个不同节目编排成节目单,要求A、B两个节目要相邻,且都不排在第4号位置,则节目单上不同的排序方式有( )
| A. | 192种 | B. | 144种 | C. | 96种 | D. | 72种 |
3.已知定义在R上的函数f(x)满足f($\sqrt{3}$)=-2,f′(x)>-$\sqrt{3}$,若x∈(0,π),则不等式f(2sinx)≤-4$\sqrt{3}$sin$\frac{x}{2}$cos$\frac{x}{2}$+1的解集( )
| A. | [$\frac{π}{3}$,$\frac{2π}{3}$] | B. | (0,$\frac{π}{3}$] | C. | [$\frac{2π}{3}$,π) | D. | (0,$\frac{π}{3}$]∪[$\frac{2π}{3}$,π) |
2.函数f(x)=log2(x+3)(x-5)的定义域是A,函数g(x)=x3+m在x∈[1,2]上的值域为B,又已知B⊆A,则实数m的取值范围是( )
| A. | (-∞,-11)∪(4,+∞) | B. | (-11,4) | C. | (-4,-3) | D. | (-∞,-4]∪[-3,+∞) |
 已知正三棱柱ABC-A1B1C1,D为AB上的中点.
已知正三棱柱ABC-A1B1C1,D为AB上的中点.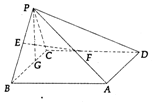 在四棱锥P-ABCD中,底面ABCD为矩形,AB⊥PC,其中BP=BC=3,PC=$\sqrt{6}$
在四棱锥P-ABCD中,底面ABCD为矩形,AB⊥PC,其中BP=BC=3,PC=$\sqrt{6}$