题目内容
1.已知:函数f(x)=x2,g(x)=2x-a,若对任意的x1∈[-1,2],存在x2∈[0,2]使得f(x1)>g(x2),则实数a的取值范围a>1.分析 对于任意的x1,总存在x2使f(x1)≥g(x2)成立成立,只需函数可以转化为f(x)min≥g(x)min,从而问题得解.
解答 解:若对任意的x1∈[-1,2],存在x2∈[0,2]使得f(x1)>g(x2),
只需f(x)min>g(x)min,
∵x1∈[-1,2],f(x)=x2∈[0,4],即f(x)min=0,
x2∈[0,2],g(x)=2x-a∈[1-a,4-a]
∴g(x)min=1-a,
∴0>1-a,
∴a>1.
故答案为:a>1.
点评 本题主要考查函数恒成立问题以及函数单调性的应用,属于对基本知识的考查,是中档题.

练习册系列答案
相关题目
6.已知集合M={0,1,2,3,4},N={1,3,5}且P=M∪N,则P的元素有( )个.
| A. | 2 | B. | 4 | C. | 6 | D. | 8 |
13.在空间直角坐标系中,一定点到三个坐标平面的距离都是2,那么该定点到原点的距离是( )
| A. | $\sqrt{6}$ | B. | $2\sqrt{3}$ | C. | $\sqrt{3}$ | D. | $\frac{{2\sqrt{6}}}{3}$ |
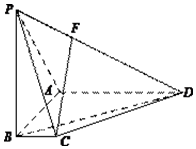 如图,在四棱锥P-ABCD中,PB⊥底面ABCD,底面ABCD为梯形,AD∥BC,AD⊥AB,且PB=AB=AD=3,BC=1.
如图,在四棱锥P-ABCD中,PB⊥底面ABCD,底面ABCD为梯形,AD∥BC,AD⊥AB,且PB=AB=AD=3,BC=1.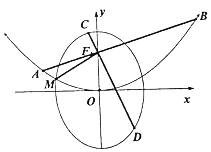 已知F1为椭圆C1:$\frac{{y}^{2}}{{a}^{2}}+\frac{{x}^{2}}{{b}^{2}}$=1的上焦点,F1也是抛物线C2:x2=4y的焦点,点M是C1与C2在第二象限的交点,且|MF1|=$\frac{5}{3}$.
已知F1为椭圆C1:$\frac{{y}^{2}}{{a}^{2}}+\frac{{x}^{2}}{{b}^{2}}$=1的上焦点,F1也是抛物线C2:x2=4y的焦点,点M是C1与C2在第二象限的交点,且|MF1|=$\frac{5}{3}$.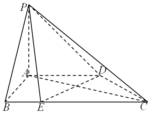 在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是直角梯形,其中AD∥BC,AB⊥AD,AB=AD=$\frac{1}{2}$BC,$\overrightarrow{BE}$=$\frac{1}{4}$$\overrightarrow{BC}$.
在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是直角梯形,其中AD∥BC,AB⊥AD,AB=AD=$\frac{1}{2}$BC,$\overrightarrow{BE}$=$\frac{1}{4}$$\overrightarrow{BC}$.