题目内容
8.已知函数f(x)=lnx+x,g(x)=$\frac{1}{2}$mx2+mx-1(m为整数).(1)求曲线y=f(x)在点(1,f(1))处的切线方程;
(2)若函数y=f(x)的图象始终在函数y=g(x)图象的下方,求m的最小值.
分析 (1)求函数的导数,利用导数的几何意义进行求解即可.
(2)构造函数G(x)=f(x)-g(x),将条件转化为G(x)<0,恒成立,求函数的导数,利用导数研究函数的最值问题即可得到结论.
解答 解:(1)函数f(x)的定义域为(0,+∞);
则f(1)=ln1+1=1,
f′(x)=1+$\frac{1}{x}$,
则f′(1)=1+1=2,
则曲线y=f(x)在点(1,f(1))处的切线方程为y-1=2(x-1),即y=2x-1;
(2)令G(x)=f(x)-g(x)=lnx-$\frac{1}{2}$mx2+(1-m)x+1,x>0,
若函数y=f(x)的图象始终在函数y=g(x)图象的下方,
等价为G(x)<0,恒成立,
即G(x)max<0恒成立,
G′(x)=$\frac{1}{x}$-mx+1-m=$\frac{-m{x}^{2}+(1-m)x+1}{x}$,(x>0),
①当m≤0时,∵x>0,∴G′(x)>0,
则G(x)在(0,+∞)上单调递增,∵G(1)=-$\frac{3}{2}$m+2>0,
∴f(x)的图象不可能在g(x)的图象的下方,
②当m>0时,G′(x)=$\frac{-m{x}^{2}+(1-m)x+1}{x}$=$\frac{-m(x-\frac{1}{m})(x+1)}{x}$,(x>0),
令G′(x)=0,得x=$\frac{1}{m}$,
当0<x<$\frac{1}{m}$时,G′(x)>0,函数G(x)递增,
当x>$\frac{1}{m}$时,G′(x)<0.函数G(x)递减,
即当x=$\frac{1}{m}$时,函数G(x)取得最大值G($\frac{1}{m}$)=ln$\frac{1}{x}$-$\frac{1}{2}$m•($\frac{1}{m}$)2+(1-m)•$\frac{1}{m}$+1=$\frac{1}{2m}$-lnm,
令r(m)=$\frac{1}{2m}$-lnm则r(m)在(0,+∞)上为减函数,
∵r(1)=$\frac{1}{2}$-ln1=$\frac{1}{2}>0$,r(2)=$\frac{1}{4}$-ln2<$\frac{1}{4}$-ln$\sqrt{e}$=-$\frac{1}{4}$<0,
∴当m≥2,r(m)<0,则m的最小值是2.
点评 本题主要考查导数的应用,求函数的导数根据导数的几何意义以及构造函数转换为最值恒成立问题是解决本题的关键.

| A. | 充要条件 | B. | 必要不充分条件 | ||
| C. | 充分不必要条件 | D. | 既不充分也不必要条件 |
| A. | a≠0,c=0 | B. | a=0,c=0 | C. | c=0 | D. | c≠0 |
| 逻辑思维能力 语言表达能力 | 一般 | 良好 | 优秀 |
| 一般 | 2 | 2 | m |
| 良好 | 4 | 4 | 1 |
| 优秀 | 1 | m | 2 |
(Ⅰ)求m,n的值;
(Ⅱ)从语言表达能力为优秀的学生中随机选取2名,求其中至少有1名逻辑思维能力优秀的学生的概率.


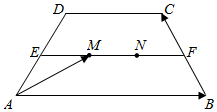 如图,已知四边形ABCD是等腰梯形,E、F分别是腰AD、BC的中点,M、N是线段EF上的两个点,且EM=MN=NF,下底是上底的2倍,若$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{BC}$=$\overrightarrow{b}$,求$\overrightarrow{AM}$.
如图,已知四边形ABCD是等腰梯形,E、F分别是腰AD、BC的中点,M、N是线段EF上的两个点,且EM=MN=NF,下底是上底的2倍,若$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{BC}$=$\overrightarrow{b}$,求$\overrightarrow{AM}$.