题目内容
19.抛物线x2=2my(m>0)的焦点为F,其准线与双曲线$\frac{x^2}{m^2}-\frac{y^2}{n^2}=1(n>0)$有两个交点A,B,若∠AFB=120°,则双曲线的离心率为3.分析 求出,F(0,$\frac{m}{2}$),准线方程为y=-$\frac{m}{2}$,代入双曲线$\frac{x^2}{m^2}-\frac{y^2}{n^2}=1(n>0)$,可得x=±$\sqrt{{m}^{2}+\frac{{m}^{4}}{4{n}^{2}}}$,利用准线与双曲线$\frac{x^2}{m^2}-\frac{y^2}{n^2}=1(n>0)$有两个交点A,B,∠AFB=120°,得出$\sqrt{{m}^{2}+\frac{{m}^{4}}{4{n}^{2}}}$=$\sqrt{3}m$,求出m,n的关系,即可得出结论.
解答 解:由题意,F(0,$\frac{m}{2}$),准线方程为y=-$\frac{m}{2}$,
代入双曲线$\frac{x^2}{m^2}-\frac{y^2}{n^2}=1(n>0)$,可得x=±$\sqrt{{m}^{2}+\frac{{m}^{4}}{4{n}^{2}}}$,
∵准线与双曲线$\frac{x^2}{m^2}-\frac{y^2}{n^2}=1(n>0)$有两个交点A,B,∠AFB=120°,
∴$\sqrt{{m}^{2}+\frac{{m}^{4}}{4{n}^{2}}}$=$\sqrt{3}m$,
∴m=2$\sqrt{2}$n,
∴双曲线的离心率为$\frac{\sqrt{8{n}^{2}+{n}^{2}}}{m}$=3.
故答案为3.
点评 本题考查抛物线、双曲线的方程与性质,考查学生的计算能力,确定m,n的关系是关键.

练习册系列答案
 小题狂做系列答案
小题狂做系列答案
相关题目
7.设向量$\overrightarrow{a}$=(2,m),$\overrightarrow{b}$=(3,-1),若$\overrightarrow{a}$⊥($\overrightarrow{a}$-2$\overrightarrow{b}$),则实数m=( )
| A. | 2或-4 | B. | 2 | C. | -$\frac{1}{4}$或$\frac{1}{2}$ | D. | -4 |
4.若集合M={x|x2-x<0},N={y|y=ax(a>0,a≠1)},R表示实数集,则下列选项错误的是( )
| A. | M∩∁RN=φ | B. | M∪N=R | C. | ∁RM∪N=R | D. | M∩N=M |
11.已知全集为R,集合A={x|x2-2x<3},B={x|x>2},则A∩(∁RB)( )
| A. | {x|-1<x<2} | B. | {x|2<x<3} | C. | {x|x<3} | D. | {x|-1<x≤2} |
9.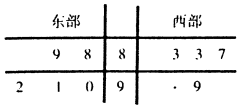 某省电视台为了解该省卫视一档成语类节目的收视情况,抽查东西两部各5个城市,得到观看该节目的人数(单位:千人)如下茎叶图所示:
某省电视台为了解该省卫视一档成语类节目的收视情况,抽查东西两部各5个城市,得到观看该节目的人数(单位:千人)如下茎叶图所示:
其中一个数字被污损.
(1)求东部各城市观看该节目观众平均人数超过西部各城市观看该节目观众平均人数的概率.
(2)随着节目的播出,极大激发了观众对成语知识的学习积累的热情,从中获益匪浅.现从观看该节目的观众中随机统计了4位观众的周均学习成语知识的时间y(单位:小时)与年龄x(单位:岁),并制作了对照表(如表所示)
由表中数据,试求线性回归方程$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$,并预测年龄为55岁观众周均学习成语知识时间.
参考公式:$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{x}^{2}}$,$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}$x.
 某省电视台为了解该省卫视一档成语类节目的收视情况,抽查东西两部各5个城市,得到观看该节目的人数(单位:千人)如下茎叶图所示:
某省电视台为了解该省卫视一档成语类节目的收视情况,抽查东西两部各5个城市,得到观看该节目的人数(单位:千人)如下茎叶图所示:其中一个数字被污损.
(1)求东部各城市观看该节目观众平均人数超过西部各城市观看该节目观众平均人数的概率.
(2)随着节目的播出,极大激发了观众对成语知识的学习积累的热情,从中获益匪浅.现从观看该节目的观众中随机统计了4位观众的周均学习成语知识的时间y(单位:小时)与年龄x(单位:岁),并制作了对照表(如表所示)
| 年龄x(岁) | 20 | 30 | 40 | 50 |
| 周均学习成语知识时间y(小时) | 2.5 | 3 | 4 | 4.5 |
参考公式:$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{x}^{2}}$,$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}$x.
 已知点P(t,$\frac{1}{2}$)在椭圆C:$\frac{{x}^{2}}{2}$+y2=1内,过P的直线l与椭圆C相交于A,B两点,且点P是线段AB的中点,O为坐标原点.
已知点P(t,$\frac{1}{2}$)在椭圆C:$\frac{{x}^{2}}{2}$+y2=1内,过P的直线l与椭圆C相交于A,B两点,且点P是线段AB的中点,O为坐标原点.