题目内容
11．已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{81}$=1（a＞0）的一条渐近线方程y=3x，则a=3．分析 根据题意，由双曲线的方程可得其渐近线方程为y=±$\frac{9}{a}$x，结合题意可得$\frac{9}{a}$=3，解可得a的值，即可得答案．
解答 解：根据题意，双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{81}$=1，则其渐近线方程为y=±$\frac{9}{a}$x，
又由题意，双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{81}$=1的一条渐近线方程y=3x，
则有$\frac{9}{a}$=3，
解可得a=3；
故答案为：3．
点评 本题考查双曲线的几何性质，关键是利用标准方程表示出渐近线方程．
练习册系列答案
相关题目
2．随着互联网经济逐步被人们接受，网上购物的人群越来越多，网上交易额也逐年增加，某地一建设银行连续五年的网银交易额统计表，如表所示：
经研究发现，年份与网银交易额之间呈线性相关关系，为了计算的方便，工作人员将上表的数据进行了处理，t=x-2011，z=y-5，得到如表：
（1）求z关于t的线性回归方程；
（2）通过（1）中的方程，求出y关于x的回归方程；
（3）用所求回归方程预测到2020年年底，该地网银交易额可达多少？
（附：在线性回归方程$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$中，$b=\frac{{\sum_{i=1}^n{{x_i}{y_i}-n\overline x\overline y}}}{{\sum_{i=1}^n{x_i^2}-n{{（\overline x）}^2}}}=\frac{{\sum_{i=1}^n{（{x_i}-\overline x）（{y_i}-\overline y}）}}{{\sum_{i=1}^n{{{（{x_i}-\overline x）}^2}}}}$，$a=\overline y-b\overline x$）
| 年份x | 2012 | 2013 | 2014 | 2015 | 2016 |
| 网上交易额y（亿元） | 5 | 6 | 7 | 8 | 10 |
| 时间代号t | 1 | 2 | 3 | 4 | 5 |
| z | 0 | 1 | 2 | 3 | 5 |
（2）通过（1）中的方程，求出y关于x的回归方程；
（3）用所求回归方程预测到2020年年底，该地网银交易额可达多少？
（附：在线性回归方程$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$中，$b=\frac{{\sum_{i=1}^n{{x_i}{y_i}-n\overline x\overline y}}}{{\sum_{i=1}^n{x_i^2}-n{{（\overline x）}^2}}}=\frac{{\sum_{i=1}^n{（{x_i}-\overline x）（{y_i}-\overline y}）}}{{\sum_{i=1}^n{{{（{x_i}-\overline x）}^2}}}}$，$a=\overline y-b\overline x$）
19．已知集合A={x|1≤x＜3}，B={x|x2≥4}，则A∩（∁RB）=（ ）
| A． | {x|1≤x＜2} | B． | {x|-2≤x＜1} | C． | {x|1≤x≤2} | D． | {x|1＜x≤2} |
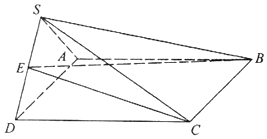如图，四棱锥S-ABCD中，底面ABCD是边长为4的正方形，平面SAD⊥平面SCD，$SA=SD=2\sqrt{2}$．
如图，在同一平面内，点P位于两平行直线l1、l2两侧，且P到l1，l2的距离分别为1，3，点M，N分别在l1，l2上，|$\overrightarrow{PM}$+$\overrightarrow{PN}$|=8，则$\overrightarrow{PM}$•$\overrightarrow{PN}$的最大值为（ ）