题目内容
在极坐标系中,ρ1+ρ2=0,θ1+θ2=π,则点M1(ρ1,θ2),M2(ρ2,θ2)的位置关系?
考点:极坐标刻画点的位置
专题:坐标系和参数方程
分析:由ρ1+ρ2=0,θ1+θ2=π,可得点M2(-ρ1,π-θ2)与点M1(ρ1,θ2)的位置关系是关于极轴对称.
解答:
解:∵ρ1+ρ2=0,θ1+θ2=π,
∴可得点M2(ρ2,θ2)即(-ρ1,π-θ2)与点M1(ρ1,θ2)的位置关系是关于极轴对称.
∴可得点M2(ρ2,θ2)即(-ρ1,π-θ2)与点M1(ρ1,θ2)的位置关系是关于极轴对称.
点评:本题考查了极坐标的对称性质,属于基础题.

练习册系列答案
相关题目
已知各项均为正数的等比数列{an},若a3=4,则log2a1+log2a5=( )
| A、1 | B、2 | C、4 | D、8 |
在圆x2+y2-2x-6y=0内,过点E(0,1)的最短弦AC的长度为( )
A、5
| ||
B、2
| ||
C、
| ||
D、20
|
设a>0,b>1,若a+b=2,则
+
的最小值为( )
| 3 |
| a |
| 1 |
| b-1 |
A、2
| ||
| B、8 | ||
C、4
| ||
D、4+2
|
已知平面向量
=(1,2),
=(2,-m)且
⊥
,则3
+2
=( )
| a |
| b |
| a |
| b |
| a |
| b |
| A、(-4,-10) |
| B、(-4,7) |
| C、(-3,-6) |
| D、(7,4) |
在等差数列{an}中,有a4+a8=a5+a7,类比上述性质,在等比数列{bn}中,有( )
| A、b4+b8=b5+b7 |
| B、b4b8=b5b7 |
| C、b4b5=b7b8 |
| D、b4b7=b5b8 |
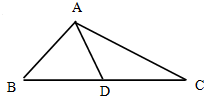 如图,在△ABC中,BC边上的中线AD长为3,且BD=2,sinB=
如图,在△ABC中,BC边上的中线AD长为3,且BD=2,sinB=