题目内容
（1）已知两正数a，b满足a+b=1．求
+
的最大值；
（2）设a＞0，b＞0，a+b+ab=24，求a+b的最小值．
| 2a+1 |
| 2b+1 |
（2）设a＞0，b＞0，a+b+ab=24，求a+b的最小值．
考点：基本不等式
专题：不等式的解法及应用
分析：（1）方法一：平方整理后，再利用ab≤（
）2=
；
方法二：利用柯西不等式即可得出；
（2）利用ab≤（
）2，转化为（a+b）2+4（a+b）-96≥0，解出即可．
| a+b |
| 2 |
| 1 |
| 4 |
方法二：利用柯西不等式即可得出；
（2）利用ab≤（
| a+b |
| 2 |
解答：
解：（1）方法一：（
+
）2=2a+1+2b+1+2
=2（a+b）+2+2
=4+2
．
∵a，b是正数，且a+b=1，∴ab≤（
）2=
，
∴（
+
）2≤8，
∴0＜
+
≤2
，
当且仅当a=b=
时，（
+
）max=2
．
方法二：
+
≤
•
=2
．
（2）a+b+ab≤a+b+(
)2，
∴a+b+(
)2≥24，
∴（a+b）2+4（a+b）-96≥0，
解得a+b≥8或a+b≤-12最小值为8．
| 2a+1 |
| 2b+1 |
| (2a+1)(2b+1) |
=2（a+b）+2+2
| 4ab+2(a+b)+1 |
| 4ab+3 |
∵a，b是正数，且a+b=1，∴ab≤（
| a+b |
| 2 |
| 1 |
| 4 |
∴（
| 2a+1 |
| 2b+1 |
∴0＜
| 2a+1 |
| 2b+1 |
| 2 |
当且仅当a=b=
| 1 |
| 2 |
| 2a+1 |
| 2b+1 |
| 2 |
方法二：
| 2a+1 |
| 2b+1 |
| 2 |
| (2a+1)2+(2b+1)2 |
| 2 |
（2）a+b+ab≤a+b+(
| a+b |
| 2 |
∴a+b+(
| a+b |
| 2 |
∴（a+b）2+4（a+b）-96≥0，
解得a+b≥8或a+b≤-12最小值为8．
点评：本题考查了基本不等式的性质、柯西不等式的性质、平方法，考查了计算能力，属于较基础题．
练习册系列答案
名校课堂系列答案
相关题目
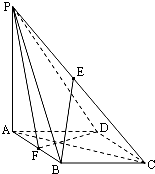如图在四棱锥P-ABCD中，底面ABCD是菱形，∠BAD=60°，AB=PA=2，PA⊥平面ABCD，E是PC的中点，F是AB中点．