题目内容
△ABC中,a,b,c分别是内角A,B,C的对边,C=
,a+b=λc,(λ>1)
(Ⅰ)若λ=
,求证:△ABC为直角三角形
(Ⅱ)若S△ABC=
λ2,且c=3,求λ.
| π |
| 3 |
(Ⅰ)若λ=
| 3 |
(Ⅱ)若S△ABC=
9
| ||
| 16 |
考点:三角形的形状判断,余弦定理
专题:解三角形
分析:(Ⅰ)依题意,a+b=λc=
c,又△ABC中,C=
,利用余弦定理可得a2+b2+2ab=3c2=3(a2+b2-2abcos
),继而可求得a=2b或b=2a,于是易判断△ABC为直角三角形;
(Ⅱ)S△ABC=
absin
=
λ2⇒ab=
λ2①,又c=3,a+b=3λ②,利用余弦定理可得λ2=4,从而可得答案.
| 3 |
| π |
| 3 |
| π |
| 3 |
(Ⅱ)S△ABC=
| 1 |
| 2 |
| π |
| 3 |
9
| ||
| 16 |
| 9 |
| 4 |
解答:
解:(Ⅰ)∵λ=
,
∴a+b=λc=
c,又△ABC中,C=
,
∴a2+b2+2ab=3c2=3(a2+b2-2abcos
),
∴(a-2b)(2a-b)=0,
∴a=2b或b=2a,
当a=2b时,
c=a+b=3b,c=
b,b2+c2=b2+3b2=4b2=a2,故△ABC为直角三角形;
当b=2a时,同理可得,a2+c2=b2,故△ABC为直角三角形;
综上所述,λ=
时,△ABC为直角三角形.
(Ⅱ)∵S△ABC=
absin
=
λ2,
∴ab=
λ2①,又c=3,∴a+b=3λ②,
∴9=c2=a2+b2-2abcos
=3c2=(a+b)2-3ab=9λ2-3×
λ2=
λ2,
∴λ2=4,λ>0,故λ=2.
| 3 |
∴a+b=λc=
| 3 |
| π |
| 3 |
∴a2+b2+2ab=3c2=3(a2+b2-2abcos
| π |
| 3 |
∴(a-2b)(2a-b)=0,
∴a=2b或b=2a,
当a=2b时,
| 3 |
| 3 |
当b=2a时,同理可得,a2+c2=b2,故△ABC为直角三角形;
综上所述,λ=
| 3 |
(Ⅱ)∵S△ABC=
| 1 |
| 2 |
| π |
| 3 |
9
| ||
| 16 |
∴ab=
| 9 |
| 4 |
∴9=c2=a2+b2-2abcos
| π |
| 3 |
| 9 |
| 4 |
| 9 |
| 4 |
∴λ2=4,λ>0,故λ=2.
点评:本题考查三角形形状的判断,突出考查余弦定理与整体代换的思想,考查综合运算能力,属于难题.

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案
相关题目
设集合P={(x,y)|x+y<4,x,y∈N*},则集合P的非空子集个数是( )
| A、2 | B、3 | C、7 | D、8 |
| a |
| a |
| b |
| a |
| b |
| 2 |
| b |
A、
| ||
B、
| ||
| C、5 | ||
| D、25 |
已知函数f﹙x﹚=|x+1|+|x+2|+…+|x+2015|+|x-1|+|x-2|+…+|x-2015|(x∈R),且f(a2-3a+2)=f(a-1),则a的值为( )
| A、1 | B、3 | C、1或4 | D、1或3 |
下列函数(1)y=πx;(2)y=2x-1;(3)y=
;(4)y=2-1-3x中,是一次函数的有( )
| 1 |
| x |
| A、4个 | B、3个 | C、2个 | D、1个 |
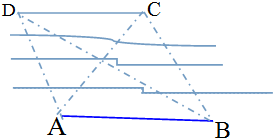 如图所示,为了测量河对岸两个建筑物C,D两点之间的距离,在河岸这边选取点A,B,测得∠BAC=45°,∠DAC=75°,∠ABD=30°,∠DBC=45°,又已知AB=
如图所示,为了测量河对岸两个建筑物C,D两点之间的距离,在河岸这边选取点A,B,测得∠BAC=45°,∠DAC=75°,∠ABD=30°,∠DBC=45°,又已知AB= 如图,已知圆O1与圆O2交于A,B两点,圆O1上的点M处切线交圆O2于D,E两点,交直线AB于点C.若CM=2,CD=1,且∠DBE=30°,则圆O2的半径为
如图,已知圆O1与圆O2交于A,B两点,圆O1上的点M处切线交圆O2于D,E两点,交直线AB于点C.若CM=2,CD=1,且∠DBE=30°,则圆O2的半径为