题目内容
已知函数f（x）=m（x+m）（2x-m-6），g（x）=（
）x-2，命题p：?x∈R，f（x）＜0或g（x）＜0．命题q：若方程f（x）=0的两根为α，β，则α＜1且β＞1．如果命题p∧q为真命题，则实数m的取值范围是（ ）
| 1 |
| 2 |
| A、（-8，-2）∪（-1，0） |
| B、（-8，-2）∪（-1，1） |
| C、（-8，-4）∪（-2，0） |
| D、（-8，-4）∪（-1，0） |
考点：复合命题的真假,一元二次方程的根的分布与系数的关系
专题：函数的性质及应用,简易逻辑
分析：根据p∧q为真命题得：p，q都为真命题．因为对于函数g（x），当x＞-1时，g（x）＜0，所以再由命题p，q可得：
，所以解不等式即可得m的取值范围．
|
解答：
解：f（x）=2mx2+m（m-6）x-m3-6m2；
∵p∧q为真命题，∴p是真命题，q是真命题；
∵对于g（x），x＞-1时，(
)x-2＜0；
由命题q知，f（x）=0有两个根，由命题p知，x≤-1时，f（x）＜0，∴m＜0 ①，且f（-1）＜0 ②；
又知道1在两根之间，∴f（1）＞0 ③；
∴由①②③得：
，解得-8＜m＜-4，或-1＜m＜0；
∴实数m的取值范围是（-8，-4）∪（-1，0）．
故选D．
∵p∧q为真命题，∴p是真命题，q是真命题；
∵对于g（x），x＞-1时，(
| 1 |
| 2 |
由命题q知，f（x）=0有两个根，由命题p知，x≤-1时，f（x）＜0，∴m＜0 ①，且f（-1）＜0 ②；
又知道1在两根之间，∴f（1）＞0 ③；
∴由①②③得：
|
∴实数m的取值范围是（-8，-4）∪（-1，0）．
故选D．
点评：本题考查指数函数的单调性，以及根据单调性解不等式，二次函数取值情况，可借助于二次函数图象是求解更形象．
练习册系列答案
阅读快车系列答案
相关题目
△ABC中，c=2，A=30°，B=120°，则△ABC的面积为（ ）
A、
| ||||
B、
| ||||
C、3
| ||||
| D、3 |
已知函数y=loga（x-1）+3（a＞0，a≠1）所过定点的横、纵坐标分别是等差数列{an}的第二项与第三项，若bn=
，数列{bn}的前n项和为Tn，则T10=（ ）
| 1 |
| an-an+1 |
A、
| ||
B、
| ||
| C、1 | ||
D、
|
下列说法正确的是（ ）
| A、三点确定一个平面 |
| B、四边形一定是平面图形 |
| C、梯形一定是平面图形 |
| D、平面和平面可能有不同在一条直线上的三个交点 |
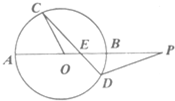如图；圆O的割线PA过圆心O交圆于另一点B，弦CD交OB于点E，且△COE～△POE，PB=OA=2，则PE的长等于（ ）