题目内容
已知tanα=
,求
的值.
| 1 |
| 2 |
| 1+2sin(π-α)cos(-2π-α) | ||
sin2(-α)-sin2(
|
考点:运用诱导公式化简求值
专题:三角函数的求值
分析:利用诱导公式以及同角三角函数的基本关系式化简表达式为正切函数的形式,代入已知条件求解即可.
解答:
解:
=
=
=
=
=
=
=-3.
| 1+2sin(π-α)cos(-2π-α) | ||
sin2(-α)-sin2(
|
=
| 1+2sinαcos(2π+α) | ||
sin2α-sin2(
|
=
| 1+2sinαcosα |
| sin2α-cos2α |
=
| sin2α+2sinαcosα+cos2α |
| (sinα-cosα)(sinα+cosα) |
=
| sinα+cosα |
| sinα-cosα |
=
| 1+tanα |
| tanα-1 |
=
1+
| ||
|
=-3.
点评:本题考查诱导公式以及同角三角函数的基本关系式的应用,基本知识的考查.

练习册系列答案
 优生乐园系列答案
优生乐园系列答案
相关题目
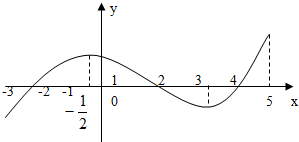 如果函数y=f(x)的导函数的图象如图所示,给出下列判断:
如果函数y=f(x)的导函数的图象如图所示,给出下列判断: