题目内容
20.关于x的方程(x2-1)2-|x2-1|-k=0,给出下列四个命题:①存在实数k,使得方程恰有2个不同的实根;
②存在实数k,使得方程恰有4个不同的实根;
③存在实数k,使得方程恰有6个不同的实根;
④存在实数k,使得方程恰有8个不同的实根.
其中真命题的个数是( )
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
分析 把已知方程变形,得k=(x2-1)2-|x2-1|,利用导数研究函数f(x)=(x2-1)2-|x2-1|的单调性,作出图象大致形状,数形结合得答案.
解答 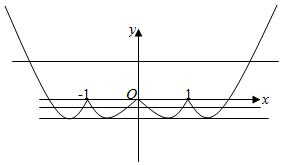 解:由(x2-1)2-|x2-1|-k=0,得k=(x2-1)2-|x2-1|,
解:由(x2-1)2-|x2-1|-k=0,得k=(x2-1)2-|x2-1|,
令f(x)=(x2-1)2-|x2-1|=$\left\{\begin{array}{l}{{x}^{4}-3{x}^{2}+2,(x≤-1或x≥1)}\\{{x}^{4}-{x}^{2},(-1<x<1)}\end{array}\right.$.
当0≤x<1时,由f(x)=x4-x2,得f′(x)=4x3-2x=2x(2x2-1),
当x∈(0,$\frac{\sqrt{2}}{2}$)时,f′(x)<0,f(x)单调递减,当x∈($\frac{\sqrt{2}}{2}$,1)时,f′(x)>0,f(x)单调递增,
f(x)有极小值为f($\frac{\sqrt{2}}{2}$)=$-\frac{1}{4}$.
当x≥1时,由f(x)=x4-3x2+2,得f′(x)=4x3-6x=2x(2x2-3),
当x∈(1,$\frac{\sqrt{6}}{2}$)时,f′(x)<0,f(x)单调递减,当x∈($\frac{\sqrt{6}}{2}$,+∞)时,f′(x)>0,f(x)单调递增
f(x)有极小值为f($\frac{\sqrt{6}}{2}$)=$-\frac{3}{4}$.
又f(x)为偶函数,作出函数f(x)的图象如图:
由图可知,直线y=k与y=f(x)的图象可以是2、4、5、8个交点.
∴正确的命题是①②④3个.
故选:D.
点评 本题主要考查了分段函数,以及函数与方程的思想,数形结合的思想,训练了利用导数研究函数的单调性与极值,属于中档题.

 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案 某高中学校为了解中学生的身高情况,从该校同年龄段的所有学生中随机抽取50名学生测量身高,由测量得到频率分布表和频率分布直方图(部分)如下:
某高中学校为了解中学生的身高情况,从该校同年龄段的所有学生中随机抽取50名学生测量身高,由测量得到频率分布表和频率分布直方图(部分)如下:| 身高 | [145,155) | [155,165) | [165,175) | [175,185) | [185,195] |
| 频数 | 3 | m | 19 | n | 4 |
(2)请用这50名学生的身高数据来估计该校这个年龄段的学生身高平均数是多少?(同一组中的数据用该组的中点值作代表);
(3)从[145,155)和[185,195]这两组中任意取出两名学生,求这两名学生身高差距超过10cm的概率.