题目内容
17.设函数f(x)=sinx-cosx,且f(α)=1,则sin2α=0.分析 由已知可得sinα-cosα=1,两边平方,利用二倍角的正弦函数公式,同角三角函数基本关系式即可得解.
解答 解:∵f(x)=sinx-cosx,且f(α)=1,
∴sinα-cosα=1,
∴两边平方,可得:sin2α+cos2α-2sinαcosα=1,
∴1-sin2α=1,可得:sin2α=0.
故答案为:0.
点评 本题主要考查了二倍角的正弦函数公式,同角三角函数基本关系式在三角函数化简求值中的应用,考查了转化思想,属于基础题.

练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
7.设随机变量ξ服从标准正态分布N(0,1),在某项测量中,已知p(|ξ|<1.96=0.950,则ξ在(-∞,-1.96)内取值的概率为( )
| A. | 0.025 | B. | 0.050 | C. | 0.950 | D. | 0.975 |
12.设a,b∈R,则“$\left\{\begin{array}{l}{a+b>2}\\{ab>1}\end{array}\right.$”是“a>1且b>1”的( )
| A. | 充分非必要条件 | B. | 必要非充分条件 | ||
| C. | 充分必要条件 | D. | 既非充分又非必要条件 |
7.已知0<a<1,logax<logay<0,则( )
| A. | 1<y<x | B. | 1<x<y | C. | x<y<1 | D. | y<x<1 |
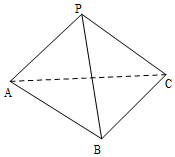 在正三棱锥P-ABC中,已知底面等边三角形的边长为6,侧棱长为4.
在正三棱锥P-ABC中,已知底面等边三角形的边长为6,侧棱长为4.