题目内容
5.已知无穷数列{an}满足an+1=$\frac{1}{2}$an(n∈N*),且a2=1,记Sn为数列{an}的前n项和,则$\underset{lim}{n→∞}$Sn=4.分析 求出等比数列的公比,然后求出数列的和,求解数列的极限即可.
解答 解:无穷数列{an}满足an+1=$\frac{1}{2}$an(n∈N*),
公比为:$\frac{1}{2}$;a2=1,a1=2,记Sn=$\frac{2(1-\frac{1}{{2}^{n}})}{1-\frac{1}{2}}$=4(1-$\frac{1}{{2}^{n}}$).
$\underset{lim}{n→∞}$Sn=$\underset{lim}{n→∞}$4(1-$\frac{1}{{2}^{n}}$)=4.
故答案为:4.
点评 本题考查数列的求和,数列极限的求法,考查计算能力.

练习册系列答案
 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
16.某赛季甲、乙两名篮球运动员每场比赛得分如图所示,则甲、乙两运动员得分的中位数分别是( )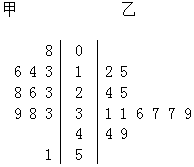

| A. | 26 33.5 | B. | 26 36 | C. | 23 31 | D. | 24.5 33.5 |