题目内容
已知直线经过点A(-2,0),B(-5,3),则该直线的倾斜角为( )
| A、150° | B、135° |
| C、75° | D、45° |
考点:直线的倾斜角
专题:直线与圆
分析:由两点式求出直线的斜率,再由斜率等于倾斜角的正切值求得直线的倾斜角.
解答:
解:∵直线经过点A(-2,0),B(-5,3),
∴其斜率k=
=-1.
设其倾斜角为θ(θ∈[0,π)),
则tanθ=-1.
∴θ=135°.
故选:B.
∴其斜率k=
| 3-0 |
| -5-(-2) |
设其倾斜角为θ(θ∈[0,π)),
则tanθ=-1.
∴θ=135°.
故选:B.
点评:本题考查了直线斜率的求法,考查了斜率和倾斜角的关系,是基础题.

练习册系列答案
相关题目
 执行如图所示的程序框图,输出的S值是( )
执行如图所示的程序框图,输出的S值是( )| A、13 | B、14 | C、15 | D、16 |
已知抛物线y2=2px过点 A(1,2),设抛物线的焦点为F,则|FA|等于( )
| A、6 | B、7 | C、5 | D、2 |
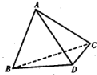 四面体ABCD中,△ABC是正三角形,△BCD是等腰直角三角形,其中BD=DC=
四面体ABCD中,△ABC是正三角形,△BCD是等腰直角三角形,其中BD=DC=