题目内容
已知椭圆C:
+
=1(a>b>0)的焦距为4,且与椭圆x2+
=1有相同的离心率,斜率为k的直线l经过点M(0,1),与椭圆C交于不同两点A、B.
(1)求椭圆C的标准方程;
(2)当椭圆C的右焦点F在以AB为直径的圆内时,求k的取值范围.
| x2 |
| a2 |
| y2 |
| b2 |
| y2 |
| 2 |
(1)求椭圆C的标准方程;
(2)当椭圆C的右焦点F在以AB为直径的圆内时,求k的取值范围.
考点:直线与圆锥曲线的关系,椭圆的标准方程,椭圆的简单性质
专题:圆锥曲线中的最值与范围问题
分析:(1)由已知得c=2,e=
=
=
,由此能求出椭圆C的标准方程.
(2)设直线l的方程为y=kx+1,A(x1,y1),B(x2,y2),由
,得(1+2k2)x2+4kx-6=0,由此利用韦达定理和向量知识结合已知条件能求出直线l的斜率k的范围.
| c |
| a |
| 2 |
| a |
| ||
| 2 |
(2)设直线l的方程为y=kx+1,A(x1,y1),B(x2,y2),由
|
解答:
解:(1)∵焦距为4,∴c=2,
又∵椭圆x2+
=1的离心率为
,
∴e=
=
=
,解得a=2
,b=2,
∴椭圆C的标准方程为
+
=1.
(2)设直线l的方程为y=kx+1,A(x1,y1),B(x2,y2),
由
,得(1+2k2)x2+4kx-6=0,
∴x1+x2=
,x1x2=
,
由(1)知右焦点F坐标为(2,0),
∵右焦点F在圆内部,∴
•
<0…(8分)
∴(x1-2)(x2-2)+y1y2<0
即x1x2-2(x1+x2)+4+k2 x1x2+k(x1+x2)+1<0…(9分)
∴(1+k2)•
+(k-2)•
+5=
<0…(11分)
∴k<
,经检验得k<
时,直线l与椭圆相交,
∴直线l的斜率k的范围为(-∞,
).…(12分)
又∵椭圆x2+
| y2 |
| 2 |
| ||
| 2 |
∴e=
| c |
| a |
| 2 |
| a |
| ||
| 2 |
| 2 |
∴椭圆C的标准方程为
| x2 |
| 8 |
| y2 |
| 4 |
(2)设直线l的方程为y=kx+1,A(x1,y1),B(x2,y2),
由
|
∴x1+x2=
| -4k |
| 1+2k2 |
| -6 |
| 1+2k2 |
由(1)知右焦点F坐标为(2,0),
∵右焦点F在圆内部,∴
| AF |
| BF |
∴(x1-2)(x2-2)+y1y2<0
即x1x2-2(x1+x2)+4+k2 x1x2+k(x1+x2)+1<0…(9分)
∴(1+k2)•
| -6 |
| 1+2k2 |
| -4k |
| 1+2k2 |
| 8k-1 |
| 1+2k2 |
∴k<
| 1 |
| 8 |
| 1 |
| 8 |
∴直线l的斜率k的范围为(-∞,
| 1 |
| 8 |
点评:本题考查椭圆的标准方程的求法,考查直线的斜率的取值范围的求法,解题时要注意函数与方程思想的合理运用.

练习册系列答案
相关题目
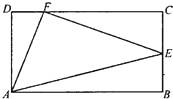 如图所示,有一个长AB=4,宽BC=2的矩形木料ABCD,E为BC的中点,点F在边CD上.一木工师傅想在该木料上取满足∠EAF=
如图所示,有一个长AB=4,宽BC=2的矩形木料ABCD,E为BC的中点,点F在边CD上.一木工师傅想在该木料上取满足∠EAF=| π |
| 3 |
A、(
| ||||
B、(
| ||||
C、(
| ||||
D、(0,
|
