题目内容
14.下列命题中正确的是( )| A. | “m=$\frac{1}{2}$”是“直线(m+2)x+3my+1=0与直线(m-2)x+(m+2)y-3=0相互平行”的充分不必要条件 | |
| B. | “直线l垂直平面α内无数条直线”是“直线l垂直于平面α”的充分条件 | |
| C. | 已知$\overrightarrow{a}$、$\overrightarrow{b}$、$\overrightarrow{c}$为非零向量,则“$\overrightarrow{a}$•$\overrightarrow{b}$=$\overrightarrow{a}$•$\overrightarrow{c}$”是“$\overrightarrow{b}$=$\overrightarrow{c}$”的充要条件 | |
| D. | p:存在x∈R,x2+2x+2 016≤0.则¬p:任意x∈R,x2+2x+2016>0. |
分析 由两直线平行与系数的关系列式求得m判断A;由线面垂直的判定判断B;由平面向量数量积的运算判断C;写出特称命题的否定判断D.
解答 解:直线(m+2)x+3my+1=0与直线(m-2)x+(m+2)y-3=0相互平行?$\left\{\begin{array}{l}{(m+2)^{2}-3m(m-2)=0}\\{-3(m+2)-(m-2)≠0}\end{array}\right.$,得m=$\frac{5±\sqrt{33}}{2}$.
∴“m=$\frac{1}{2}$”是“直线(m+2)x+3my+1=0与直线(m-2)x+(m+2)y-3=0相互平行”的既不充分也不必要条件,故A错误;
直线l垂直平面α内无数条直线,不一定有直线垂直平面,∴“直线l垂直平面α内无数条直线”不是“直线l垂直于平面α”的充分条件,故B错误;
$\overrightarrow{a}$、$\overrightarrow{b}$、$\overrightarrow{c}$为非零向量,由$\overrightarrow{a}$•$\overrightarrow{b}$=$\overrightarrow{a}$•$\overrightarrow{c}$不能得到$\overrightarrow{b}$=$\overrightarrow{c}$,反之,由$\overrightarrow{b}$=$\overrightarrow{c}$能够得到$\overrightarrow{a}$•$\overrightarrow{b}$=$\overrightarrow{a}$•$\overrightarrow{c}$,∴“$\overrightarrow{a}$•$\overrightarrow{b}$=$\overrightarrow{a}$•$\overrightarrow{c}$”是“$\overrightarrow{b}$=$\overrightarrow{c}$”的必要不充分条件,故C错误;
p:存在x∈R,x2+2x+2 016≤0.则¬p:任意x∈R,x2+2x+2016>0,故D正确.
故选:D.
点评 本题考查命题的真假判断与应用,考查了充分必要条件的判定方法,考查特称命题的否定,是基础题.

 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案| A. | 2人 | B. | 3人 | C. | 2人或3人 | D. | 4人 |
| A. | 700 | B. | 300 | C. | 400 | D. | 12 |
| A. | 3 | B. | 5 | C. | $\sqrt{26}$ | D. | $\sqrt{29}$ |
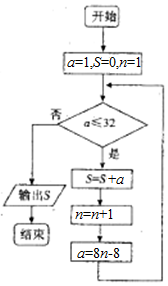 我国古代数学著作《孙子算经》中有如下的问题:“今有方物一束,外周有三十二枚,问积几何?”设每层外周枚数为a,如图是解决该问题的程序框图,则输出的结果为( )
我国古代数学著作《孙子算经》中有如下的问题:“今有方物一束,外周有三十二枚,问积几何?”设每层外周枚数为a,如图是解决该问题的程序框图,则输出的结果为( )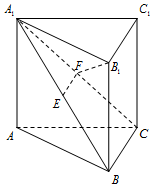 如图,在直三棱柱ABC-A1B1C1中,A1B1⊥B1C1,E、F分别是A1B、A1C的中点.
如图,在直三棱柱ABC-A1B1C1中,A1B1⊥B1C1,E、F分别是A1B、A1C的中点.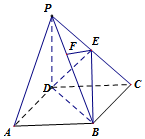 在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,点E是PC的中点,作EF⊥PB交PB于点F.
在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,点E是PC的中点,作EF⊥PB交PB于点F.