题目内容
9.已知数列{xn}满足xn+2=|xn+1-xn|(n∈N*),若x1=1,x2=a(a≤1,a≠0),且xn+3=xn对于任意正整数n均成立,则数列{xn}的前2016项和S2016的值为( )| A. | 672 | B. | 673 | C. | 1342 | D. | 1344 |
分析 x1=1,x2=a(a≤1,a≠0),可得x3=|x2-x1|=|a-1|=1-a,x1+x2+x3=1+a+(1-a)=2;xn+3=xn对于任意正整数n均成立,可得数列{xn}的周期为3,即可得出.
解答 解:∵x1=1,x2=a(a≤1,a≠0),∴x3=|x2-x1|=|a-1|=1-a,∴x1+x2+x3=1+a+(1-a)=2;
xn+3=xn对于任意正整数n均成立,∴数列{xn}的周期为3,
数列{xn}的前2016项和S2016的值=672×2=1344.
故答案为:D.
点评 本题考查了数列递推关系、数列的周期性、数列求和,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
19.设复数z满足z+i=i(2-i),则$\overline{z}$=( )
| A. | 1+3i | B. | -1+3i | C. | 1-i | D. | -1+i |
17.已知三棱锥P-ABC中,PA⊥底面ABC,AB⊥BC,PA=AC=2,且该三棱锥所有顶点都在球O的球面上,则球O的表面积为( )
| A. | 4π | B. | 8π | C. | 16π | D. | 20π |
4.已知平面向量$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow c$满足|$\overrightarrow{a}$|=|$\overrightarrow{b}$|=1,$\overrightarrow{a}$⊥($\overrightarrow{a}$-2$\overrightarrow{b}$),$(\overrightarrow c-2\overrightarrow a)•(\overrightarrow c-\overrightarrow b)=0$,则|$\overrightarrow c$|的最大值为( )
| A. | 0 | B. | $\sqrt{3}$ | C. | $\frac{\sqrt{7}+\sqrt{3}}{2}$ | D. | $\sqrt{7}$ |
19.函数$y=sin(2x+\frac{π}{3})$的图象经过下列平移,可以得到函数$y=cos(2x+\frac{π}{6})$图象的是( )
| A. | 向右平移$\frac{π}{6}$个单位 | B. | 向左平移$\frac{π}{6}$个单位 | ||
| C. | 向右平移$\frac{π}{3}$个单位 | D. | 向左平移$\frac{π}{3}$个单位 |
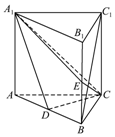 如图,直三棱柱ABC-A1B1C1中,D,E分别是AB,BB1的中点,AA1=AC=CB=2,AB=2$\sqrt{2}$.
如图,直三棱柱ABC-A1B1C1中,D,E分别是AB,BB1的中点,AA1=AC=CB=2,AB=2$\sqrt{2}$.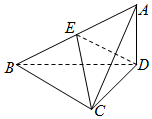 已知三棱锥A-BCD中,△ABC是等腰直角三角形,且AC⊥BC,BC=2,AD⊥平面BCD,AD=1.
已知三棱锥A-BCD中,△ABC是等腰直角三角形,且AC⊥BC,BC=2,AD⊥平面BCD,AD=1. 如图在直角梯形BB1C1C中,∠CC1B1=90°,BB1∥CC1,CC1=B1C1=2BB1=2,D是CC1的中点.四边形AA1C1C可以通过直角梯形BB1C1C以CC1为轴旋转得到,且二面角B1-CC1-A为120°.
如图在直角梯形BB1C1C中,∠CC1B1=90°,BB1∥CC1,CC1=B1C1=2BB1=2,D是CC1的中点.四边形AA1C1C可以通过直角梯形BB1C1C以CC1为轴旋转得到,且二面角B1-CC1-A为120°.