题目内容
4.已知函数f(x)=x-lnx,g(x)=x3+x2f(x)-16x+20.(Ⅰ)求f(x)的单调区间及极值;
(Ⅱ)求证:g(x)的图象恒在x轴的上方.
分析 (Ⅰ)求导,令f′(x)=0,根据导数与函数单调性的关系,即可求得f(x)的单调区间及极值;
(Ⅱ)由(Ⅰ)可知:g(x)≥x3+x2-16x+20,等号当且仅当x=1时成立.构造辅助函数,求导,利用导数与函数单调性的关系,求得g(x)>0,即可证明g(x)的图象恒在x轴的上方.
解答 解:(Ⅰ)函数f(x)的定义域为(0,+∞),$f'(x)=\frac{x-1}{x}(x>0)$.
令$f'(x)=\frac{x-1}{x}=0$,得x=1.
令f'(x)>0得x>1,f(x)递增;令f'(x)<0得0<x<1,f(x)递减.
∴f(x)的增区间为(1,+∞),减区间为(0,1),
∴f(x)的极小值为f(1)=1,f(x)无极大值.…(5分)
(Ⅱ)证明:由(Ⅰ)知f(x)≥1,
∴g(x)≥x3+x2-16x+20,等号当且仅当x=1时成立.
设h(x)=x3+x2-16x+20,则h'(x)=3x2+2x-16=(3x+8)(x-2),
令h'(x)>0得x>2;
令h'(x)<0,得0<x<2.
∴h(x)min=h(2)=0,
∴h(x)≥0,等号当且仅当x=2时成立.
因为取等号不一样,所以g(x)>0
即g(x)的图象恒在x轴的上方.…(12分)
点评 本题考查导数的综合应用,考查利用导数求函数的单调区间及最值,考查转化思想,属于中档题.

练习册系列答案
相关题目
14.某五国领导人A,B,C,D,E参加国际会议,除E与B,E与D不单独会晤外,其他领导人两两之间都要单独会晤,现安排他们在两天的上午、下午单独会晤(每人每个半天最多进行一次会晤),那么安排他们单独会晤的不同方法共有( )
| A. | 48种 | B. | 36种 | C. | 24种 | D. | 8种 |
19.已知△ABC中,BC=$\sqrt{3}$,AC=2,角A=60°,则边AB=( )
| A. | $\sqrt{3}$ | B. | 2 | C. | 1 | D. | $\sqrt{3}+\frac{1}{2}$ |
9.质点M的运动方程S=2t2-2为 则在时间段[2,2+△t]内的平均速度为( )
| A. | 8+2△t | B. | 4+2+△t | C. | 7+2+△t | D. | -8+2+△t |
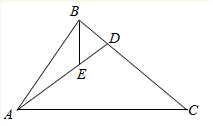 如图,在△ABC中,已知∠BAC=$\frac{π}{3}$,|$\overrightarrow{AB}$|=2,|$\overrightarrow{AC}$|=3,点D为边BC上一点,满足$\overrightarrow{AC}$+2$\overrightarrow{AB}$=3$\overrightarrow{AD}$,点E是AD上一点,满足$\overrightarrow{AE}$=2$\overrightarrow{ED}$,则|$\overrightarrow{BE}$|=$\frac{2\sqrt{19}}{9}$.
如图,在△ABC中,已知∠BAC=$\frac{π}{3}$,|$\overrightarrow{AB}$|=2,|$\overrightarrow{AC}$|=3,点D为边BC上一点,满足$\overrightarrow{AC}$+2$\overrightarrow{AB}$=3$\overrightarrow{AD}$,点E是AD上一点,满足$\overrightarrow{AE}$=2$\overrightarrow{ED}$,则|$\overrightarrow{BE}$|=$\frac{2\sqrt{19}}{9}$.