题目内容
1.已知等差数列{an}的前n项和为Sn,首项为1的等比数列{bn}的公比为q,S2=a3=b3,且a1,a3,b4成等比数列.(1)求{an}和{bn}的通项公式;
(2)设${c_n}=k+{a_n}+{log_3}{b_n}(k∈N_{\;}^+),若\frac{1}{c_1},\frac{1}{c_2},\frac{1}{c_t}$(t≥3)成等差数列,求k和t的值.
分析 (1)设等差数列{an}的公差为d,运用等差数列和等比数列的通项公式,以及等比数列中项的性质,可得方程,解方程可得公差、公比及首项,进而得到所求通项公式;
(2)求得cn=k+an+log3bn=k+3n+log33n-1=k+4n-1,由等差数列中项的性质,可得$\frac{2}{k+7}$=$\frac{1}{k+3}$+$\frac{1}{k+4t-1}$,化简可得t=3+$\frac{8}{k-1}$,讨论k的取值,可得t的值.
解答 解:(1)设等差数列{an}的公差为d,由S2=a3=b3,
可得2a1+d=a1+2d=b1q2=q2,①
a1,a3,b4成等比数列,可得
a32=a1b4,即(a1+2d)2=a1(b1q3)=a1q3,②
由①②可得a1=d=q=3,
则an=3+3(n-1)=3n,bn=3n-1,n∈N*;
(2)cn=k+an+log3bn=k+3n+log33n-1=k+4n-1,
则c1=k+3,c2=k+7,ct=k+4t-1,
由$\frac{1}{{c}_{1}}$,$\frac{1}{{c}_{2}}$,$\frac{1}{{c}_{t}}$(t≥3)成等差数列,可得
$\frac{2}{{c}_{2}}$=$\frac{1}{{c}_{1}}$+$\frac{1}{{c}_{t}}$,即为$\frac{2}{k+7}$=$\frac{1}{k+3}$+$\frac{1}{k+4t-1}$,
化简可得t=3+$\frac{8}{k-1}$,
由t≥3,且t∈N*,可得k-1为8的正约数,
即有k=2,t=11或k=3,t=7或k=5,t=5或k=9,t=4.
点评 本题考查等差数列和等比数列的通项公式和求和公式的运用,等差数列中项的性质,考查方程思想,以及分类讨论的思想方法,化简整理的运算能力,属于中档题.

| A. | 8+2△t | B. | 4+2+△t | C. | 7+2+△t | D. | -8+2+△t |
| A. | {x|x≤-1} | B. | {x|x≥3} | C. | $\{x|x<-\frac{5}{4}\}$ | D. | $\{x|-\frac{5}{4}≤x<-1\}$ |
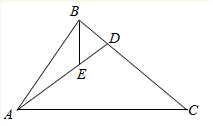 如图,在△ABC中,已知∠BAC=$\frac{π}{3}$,|$\overrightarrow{AB}$|=2,|$\overrightarrow{AC}$|=3,点D为边BC上一点,满足$\overrightarrow{AC}$+2$\overrightarrow{AB}$=3$\overrightarrow{AD}$,点E是AD上一点,满足$\overrightarrow{AE}$=2$\overrightarrow{ED}$,则|$\overrightarrow{BE}$|=$\frac{2\sqrt{19}}{9}$.
如图,在△ABC中,已知∠BAC=$\frac{π}{3}$,|$\overrightarrow{AB}$|=2,|$\overrightarrow{AC}$|=3,点D为边BC上一点,满足$\overrightarrow{AC}$+2$\overrightarrow{AB}$=3$\overrightarrow{AD}$,点E是AD上一点,满足$\overrightarrow{AE}$=2$\overrightarrow{ED}$,则|$\overrightarrow{BE}$|=$\frac{2\sqrt{19}}{9}$.