题目内容
9.已知f(x,y)=ax+by,若1≤f(1,1)≤2且-1≤f(1,-1)≤1,则f(2,1)的取值范围为$[{1\;,\;\;\frac{7}{2}}]$.分析 求出约束条件,目标函数,利用线性规划求解即可.
解答  解:f(x,y)=ax+by,若1≤f(1,1)≤2且-1≤f(1,-1)≤1,
解:f(x,y)=ax+by,若1≤f(1,1)≤2且-1≤f(1,-1)≤1,
可得$\left\{\begin{array}{l}{1≤a+b≤2}\\{-1≤a-b≤1}\end{array}\right.$,画出不等式组的可行域如图:
则f(2,1)=2a+b,当直线z=2a+b经过A时取得最小值,经过B时取得最大值,
由$\left\{\begin{array}{l}{a+b=2}\\{a-b=1}\end{array}\right.$可得B($\frac{3}{2}$,$\frac{1}{2}$),
f(2,1)=2a+b的最小值为:!,最大值为:$\frac{7}{2}$.
故答案为:$[{1\;,\;\;\frac{7}{2}}]$.
点评 本题考查线性规划的简单应用,画出可行域是解题的关键.

练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目
19.一个平面四边形的斜二测画法的直观图是一个边长为1的正方形,则原平面四边形的面积等于( )
| A. | $\sqrt{2}$ | B. | $2\sqrt{2}$ | C. | $\frac{{8\sqrt{2}}}{3}$ | D. | $8\sqrt{2}$ |
17.由于电子技术的飞速发展,计算机的成本不断降低,若每隔5年计算机的价格降低$\frac{1}{3}$,现在价格为8100元的计算机经过15年的价格应降为( )
| A. | 2300元 | B. | 2800元 | C. | 2400元 | D. | 2000元 |

 上随机取一个数
上随机取一个数 ,则
,则 的概率为 。
的概率为 。 .
.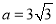 ,
,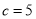 ,求b
,求b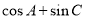 的取值范围.
的取值范围.