题目内容

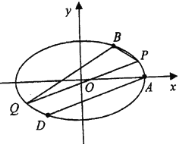
【题目】已知椭圆的右焦点为.直线被称作为椭圆的一条准线.点在椭圆上(异于椭圆左、右顶点)，过点作直线与椭圆相切，且与直线相交于点.

（1）求证：.

（2）若点在轴的上方，，求面积的最小值.

【答案】（1）见解析；（2）1

【解析】

（1）联立直线的方程和椭圆的方程，利用判别式列方程，求得点的坐标，求得点的坐标，通过计算得到，由此证得.

（2）求得，由此求得三角形面积的表达式，根据函数的单调性求得三角形面积的最小值.

(1)点的坐标为.

联立方程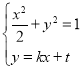,消去后整理为

有,可得，，.

可得点的坐标为.

当时，可求得点的坐标为，

，.

有.

故有.

(2)若点在轴上方，必有

由(1)知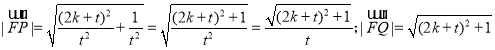

因为时.由(1)知，，

由函数单调递增，可得此时.

故当时，的面积取得最小值为1.

练习册系列答案
相关题目

【题目】为迎接2022年冬奥会，某市组织中学生开展冰雪运动的培训活动，并在培训结束后对学生进行了考核.记表示学生的考核成绩，并规定为考核优秀.为了了解本次培训活动的效果，在参加培训的学生中随机抽取了30名学生的考核成绩，并作成如图所示的茎叶图：

（1）从参加培训的学生中随机选取1人，请根据图中数据，估计这名学生考核为优秀的概率；

（2）从图中考核成绩满足的学生中任取3人，设表示这3人中成绩满足的人数，求的分布列和数学期望；

（3）根据以往培训数据，规定当时培训有效.请你根据图中数据，判断此次冰雪培训活动是否有效，并说明理由.

【题目】已知抛物线与过点的直线交于两点.

（1）若，求直线的方程；

（2）若，轴，垂足为，探究：以为直径的圆是否过定点？若是，求出该定点的坐标；若不是，请说明理由.

【题目】某校在圆心角为直角，半径为的扇形区域内进行野外生存训练.如图所示，在相距的，两个位置分别为300,100名学生，在道路上设置集合地点，要求所有学生沿最短路径到点集合，记所有学生进行的总路程为.

（1）设，写出关于的函数表达式；

（2）当最小时，集合地点离点多远？

【题目】已知椭圆：的右顶点为，离心率为，点在椭圆上，点与点关于原点对称.

（1）求椭圆的标准方程；

（2）求经过点，且和轴相切的圆的方程；

（3）若，是椭圆上异于，的两个点，且，点在直线的上方，试判断的平分线是否经过轴上的一个定点？若是，求出该定点坐标；若不是，请说明理由.

【题目】若存在，使得对任意恒成立，则函数在上有下界，其中为函数的一个下界；若存在，使得对任意恒成立，则函数在上有上界，其中为函数的一个上界．如果一个函数既有上界又有下界，那么称该函数有界．

下述四个结论：①1不是函数的一个下界；②函数有下界，无上界；③函数有上界，无下界；④函数有界．

其中所有正确结论的编号是（ ）

A.①②B.②④C.③④D.②

【题目】已知向量.

（1）求f(x)的单调递增区间；

（2）在△ABC中，角A，B，C的对边分别为a，b，c，且，若f(A)=1，求△ABC的周长.

【题目】已知，分别为椭圆的左、右焦点，点在椭圆上，且轴，的周长为6.

（Ⅰ）求椭圆的标准方程；

（Ⅱ）过点的直线与椭圆交于，两点，设为坐标原点，是否存在常数，使得恒成立？请说明理由.

【题目】已知是定义在上的偶函数，其图象关于点对称.以下关于的结论：①是周期函数；②满足；③在单调递减；④是满足条件的一个函数.其中正确结论的个数是( )

A.4B.3C.2D.1

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网