题目内容
17.抛物线M的顶点是坐标原点O,抛物线M的焦点F在x轴正半轴上,抛物线M的准线与曲线x2+y2-6x+4y-3=0只有一个公共点,设A是抛物线M上的一点,若$\overrightarrow{OA}$•$\overrightarrow{AF}$=-4,则点A的坐标是( )| A. | (-1,2)或(-1,-2) | B. | (1,2)或(1,-2) | C. | (1,2) | D. | (1,-2) |
分析 先求出抛物线的焦点F(1,0),根据抛物线的方程设A($\frac{{{y}_{0}}^{2}}{4}$,y0),则$\overrightarrow{OA}$=($\frac{{{y}_{0}}^{2}}{4}$,y0),$\overrightarrow{AF}$=(1-$\frac{{{y}_{0}}^{2}}{4}$,-y0),再由$\overrightarrow{OA}$•$\overrightarrow{AF}$=-4,可求得y0的值,最后可得答案.
解答 解:x2+y2-6x+4y-3=0,可化为(x-3)2+(y+2)2=16,圆心坐标为(3,-2),半径为4,
∵抛物线M的准线与曲线x2+y2-6x+4y-3=0只有一个公共点,
∴3+$\frac{p}{2}$=4,∴p=2.
∴F(1,0),
设A($\frac{{{y}_{0}}^{2}}{4}$,y0)
则$\overrightarrow{OA}$=($\frac{{{y}_{0}}^{2}}{4}$,y0),$\overrightarrow{AF}$=(1-$\frac{{{y}_{0}}^{2}}{4}$,-y0),
由$\overrightarrow{OA}$•$\overrightarrow{AF}$=-4,∴y0=±2,∴A(1,±2)
故选B.
点评 本题主要考查抛物线的标准方程,考查直线与圆的位置关系,考查向量知识的运用,属于中档题.

练习册系列答案
 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案
相关题目
2.为了普及法律知识,达到“法在心中”的目的,某市法制办组织了一次普法知识竞赛.统计局调查队从甲、乙两单位中各随机抽取了5名职工的成绩,如下:
(1)根据表中的数据,分别求出样本中甲、乙两单位职工成绩的平均数和方差,并判断哪个单位职工对法律知识的掌握更为稳定;
(2)用简单随机抽样的方法从乙单位的5名职工中抽取2名,他们的成绩组成一个样本,求抽取的2名职工的成绩之差的绝对值至少是4分的概率.
| 甲单位职工的成绩(分) | 87 | 88 | 91 | 91 | 93 |
| 乙单位职工的成绩(分) | 85 | 89 | 91 | 92 | 93 |
(2)用简单随机抽样的方法从乙单位的5名职工中抽取2名,他们的成绩组成一个样本,求抽取的2名职工的成绩之差的绝对值至少是4分的概率.
6.已知集合A={x|x≥2,或x≤-1},B={x|log3(2-x)≤1},则A∩(∁RB)=( )
| A. | {x|x<-1} | B. | {x|x≤-1,或x>2} | C. | {x|x≥2,或x=-1} | D. | {x|x<-1,或x≥2} |
7.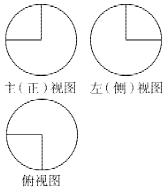 如图,某几何体的三视图是三个半径相等的圆及每个圆中两条相互垂直的半径,若该几何体的表面积是17π,则它的体积是( )
如图,某几何体的三视图是三个半径相等的圆及每个圆中两条相互垂直的半径,若该几何体的表面积是17π,则它的体积是( )
 如图,某几何体的三视图是三个半径相等的圆及每个圆中两条相互垂直的半径,若该几何体的表面积是17π,则它的体积是( )
如图,某几何体的三视图是三个半径相等的圆及每个圆中两条相互垂直的半径,若该几何体的表面积是17π,则它的体积是( )| A. | 8π | B. | $\frac{56π}{3}$ | C. | $\frac{14π}{3}$ | D. | $\frac{28π}{3}$ |