题目内容
6.计算由曲线y2=x和直线y=x-2所围成的图形的面积是( )| A. | $\frac{11}{2}$ | B. | 18 | C. | $\frac{23}{6}$ | D. | $\frac{9}{2}$ |
分析 先求出曲线y2=2x 和直线y=x-2的交点坐标,从而得到积分的上下限,然后利用定积分表示出图形面积,最后根据定积分的定义求出即可.
解答 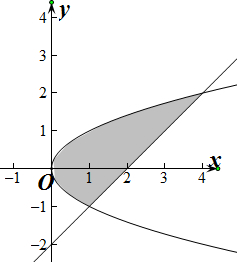 解:联立方程组得$\left\{\begin{array}{l}{{y}^{2}=x}\\{y=x-2}\end{array}\right.$解得曲线y2=x和直线y=x-2的交点坐标为:(1,-1),(4,2),
解:联立方程组得$\left\{\begin{array}{l}{{y}^{2}=x}\\{y=x-2}\end{array}\right.$解得曲线y2=x和直线y=x-2的交点坐标为:(1,-1),(4,2),
选择y为积分变量,
∴由曲线y2=x和直线y=x-2所围成的图形的面积S=${∫}_{-1}^{2}$(y+2-y2)dy=$(\frac{1}{2}{y}^{2}+2y-\frac{1}{3}{y}^{3})$|${\;}_{-1}^{2}$=(2+4-$\frac{8}{3}$)-($\frac{1}{2}$-2+$\frac{1}{3}$)=$\frac{9}{2}$
点评 本题主要考查了定积分在求面积中的应用,以及会利用定积分求图形面积的能力.应用定积分求平面图形面积时,积分变量的选取是至关重要的,属于基础题.

练习册系列答案
相关题目
18.已知直线l经过点A(1,-2),B(-3,2),则直线l的方程是( )
| A. | x+y+1=0 | B. | x-y+1=0 | C. | x+2y+1=0 | D. | x+2y-1=0 |
1.设函数f(x)定义在实数集上,f(1+x)=f(1-x),且当x≥1时,$f(x)={({\frac{1}{2}})^x}$,则有( )
| A. | $f({\frac{1}{3}})<f(2)<f({\frac{1}{2}})$ | B. | $f({\frac{1}{2}})<f(2)<f({\frac{1}{3}})$ | C. | $f({\frac{1}{2}})<f({\frac{1}{3}})<f(2)$ | D. | $f(2)<f({\frac{1}{3}})<f({\frac{1}{2}})$ |
11.若△ABC的三边为a,b,c,它的面积为$\frac{1}{4}$(a2+b2-c2),那么内角C等于( )
| A. | 30° | B. | 90° | C. | 60° | D. | 45° |
18.数列2014,2015,1,-2014,…;从第二项起,每一项都等于它的前后两项之和,则该数列的前2015项之和等于( )
| A. | 2014 | B. | 2015 | C. | 1 | D. | 0 |