不等式|x-1|-|x-4|＞2的解集为{x|x＞$\frac{7}{2}$}．题目和参考答案——青夏教育精英家教网——

题目内容

1．不等式|x-1|-|x-4|＞2的解集为{x|x＞$\frac{7}{2}$}．

分析根据|x-1|-|x-4|表示数轴上的x对应点到1对应点的距离减去它到4对应点的距离，而$\frac{7}{2}$到1对应点的距离减去它到4对应点的距离正好等于2，由此可得不等式的解集．

解答解：由于|x-1|-|x-4|表示数轴上的x对应点到1对应点的距离减去它到4对应点的距离，
而$\frac{7}{2}$到1对应点的距离减去它到4对应点的距离正好等于2，
故不等式|x-1|-|x-4|＞2的解集为：{x|x＞$\frac{7}{2}$}，
故答案为：{x|x＞$\frac{7}{2}$}．

点评本题主要考查绝对值的意义，绝对值不等式的解法，属于中档题．

练习册系列答案

湘教考苑单元测试卷系列答案

精美课堂系列答案

高中同步创新课堂优化方案系列答案

希望全程检测单元测试卷系列答案

全程培优卷系列答案

名师点拨卷系列答案

期末模拟16套系列答案

特优五合卷系列答案

英才计划期末调研系列答案

新课堂冲刺100分系列答案

相关题目

11．用秦九韶算法求多项式f（x）=4x⁴+3x³+2x²+x+7的值，则f（2）的值为（　　）

12．已知函数$f（x）=\frac{{\sqrt{a}x+b}}{{1+{x^2}}}$是定义在（-1，1）上的奇函数，且$f（\frac{1}{2}）=\frac{2}{5}$．
（1）求实数a，b的值；
（2）判断并证明f（x）在（-1，1）上的单调性．

9．复数$\frac{2-i}{1-i}$的共轭复数是（　　）

$\frac{3+i}{2}$

$\frac{1-i}{2}$

$\frac{3-i}{2}$

$\frac{-3-i}{2}$

16．在锐角△ABC中，角A，B，C所对的边分别为a，b，c，若$sinA=\frac{{2\sqrt{2}}}{3}$，a=2，ccosB+bcosC=2acosB，则b的值为（　　）

$\frac{{3\sqrt{2}}}{4}$

$\frac{{3\sqrt{3}}}{4}$

$\frac{{3\sqrt{6}}}{4}$

6．（1）计算${（5\frac{1}{16}）^{0.5}}-2×{（2\frac{10}{27}）^{-\frac{2}{3}}}-2×{（\sqrt{2+π}）^0}÷{（\frac{3}{4}）^{-2}}$
（2）计算${9^{{{log}_3}2}}-4{log_4}3•{log_{27}}8+\frac{1}{3}{log_6}8-2{log_{{6^{-1}}}}\sqrt{3}$．

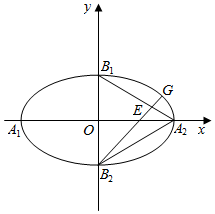如图，已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的四个顶点是A₁，A₂，B₁，B₂，△A₂B₁B₂是边长为2的正三角形．
（1）求椭圆的方程；
（2）若G是椭圆上在第一象限内的动点，直线B₁G交线段A₂B₂于点E，求$\frac{|G{B}_{1}|}{|E{B}_{1}|}$的取值范围．

10．某几何体的三视图如图所示，则该几何体的体积是6-$\frac{2π}{3}$．

11．直线3x+4y+2^m=0与圆x²+（y-$\frac{1}{2}$）²=1相切，且实数m的值为（　　）