题目内容
10.某企业的4名职工参加职业技能考核,每名职工均可从4个备选考核项目中任意抽取一个参加考核,则恰有一个项目未被抽中的概率是$\frac{9}{16}$.分析 先求出基本事件总数n=44,再求出恰有一个项目未被抽中包含的基本事件个数,由此能求出恰有一个项目未被抽中的概率.
解答 解:解:某企业的4名职工参加职业技能考核,每名职工均可从4个备选考核项项目中任意抽取一个参加考核,
基本事件总数n=44,
恰有一个项目未被抽中包含的基本事件个数为:m=${C}_{4}^{2}•{A}_{4}^{4}$,
∴恰有一个项目未被抽中的概率为p=$\frac{m}{n}$=$\frac{{C}_{4}^{2}{A}_{4}^{4}}{{4}^{4}}$=$\frac{9}{16}$.
故答案为:$\frac{9}{16}$.
点评 本题考查概率的求法,考查古典概型的概率计算,属于基础题,解题时要注意等可能事件概率计算公式的合理运用.

练习册系列答案
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案
相关题目
1.阅读如图程序框图,当输入x的值为2时,运行相应程序,则输出x的值为( )


| A. | 5 | B. | 11 | C. | 23 | D. | 47 |
15.已知集合$M=\left\{{x\left|{\frac{x-5}{x+1}≤0}\right.}\right\}$,N={-3,-1,1,3,5},则M∩N=( )
| A. | {-3,-1,1,3,5} | B. | {-1,1,3,5} | C. | {1,3,5} | D. | {-3,-1,1,3,} |
2.如图所示,图中粗线画出的是某几何体的三视图,该几何体的体积是( )
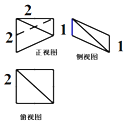

| A. | $\frac{2}{3}$ | B. | $\frac{4}{3}$ | C. | $\frac{8}{3}$ | D. | 4 |
20.已知奇函数f(x)在[0,+∞)上是增函数,若f(lnx)<0,则( )
| A. | $\frac{1}{e}$<x<1或x>1 | B. | 1<x<e | C. | 0<x<e或x>e | D. | 0<x<1 |




