题目内容
已知向量
=（1，-1），
=（-2，t），若（2
-
）⊥
，则t= ．
| a |
| b |
| a |
| b |
| a |
考点：平面向量数量积的运算
专题：平面向量及应用
分析：求出2
-
的坐标，利用（2
-
）⊥
，数量积为0，得到关于t的等式解之．
| a |
| b |
| a |
| b |
| a |
解答：
解：由已知，2
-
=（4，-2-t），又（2
-
）⊥
，所以（2
-
）•
=0，即4+2+t=0，解得t=-6；
故答案为：-6．
| a |
| b |
| a |
| b |
| a |
| a |
| b |
| a |
故答案为：-6．
点评：本题考查了向量的加减的坐标运算以及向量垂直的性质．
练习册系列答案
相关题目
已知全集I={0，1，2，3，4}，集合M={1，2，3}，N={0，3]，则（∁IM）∪N=（ ）
| A、{0，3，4} |
| B、{0} |
| C、{0，1，2，3} |
| D、{0，1，2，3，4} |
如图所示，程序框图输出的所有实数对（x，y）所对应的点都在函数（ ）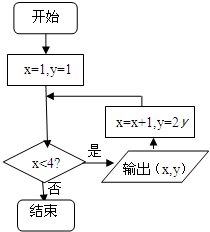
| A、y=x+1的图象上 |
| B、y=2x的图象上 |
| C、y=2x的图象上 |
| D、y=2x-1的图象上 |
已知
与
为互相垂直的单位向量，
=
-2
，
=
+λ
且
与
的夹角为锐角，则实数λ的取值范围是（ ）
| i |
| j |
| a |
| i |
| j |
| b |
| i |
| j |
| a |
| b |
A、（-∞，
| ||||
B、（
| ||||
C、（-2，
| ||||
D、（-∞，-2）∪（-2，
|