题目内容
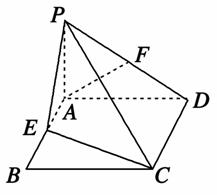
如图,在几何体P-ABCD中,四边形ABCD为矩形,PA⊥平面ABCD,AB=PA=2.
(1)当AD=2时,求证:平面PBD⊥平面PAC;
(2)若PC与AD所成的角为45°,求几何求P-ABCD的体积.
[解析] (1)证明:当AD=2时,四边形ABCD是正方形,则BD⊥AC.
∵PA⊥平面ABCD,BD平面ABCD,
∴PA⊥BD.
又∵PA∩AC=A,∴BD⊥平面PAC.
∵BD平面PBD,
∴平面PBD⊥平面PAC.
(2)解:PC与AD成45°角,AD∥BC,
则∠PCB=45°.
∵BC⊥AB,BC⊥PA,AB∩PA=A,
∴BC⊥平面PAB,PB平面PAB.
∴BC⊥PB.
∴∠CPB=90°-45°=45°.
∴BC=PB=2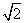 .
.
∴几何体P-ABCD的体积为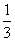 ×(2×2
×(2×2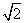 )×2=
)×2=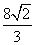 .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
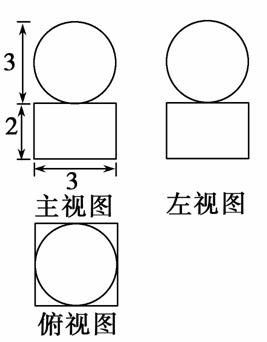
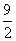 π+12 B.
π+12 B.
 B.
B. C.
C.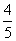 D.
D.
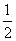 (AC+BD)(填“>”,“<”或“=”).
(AC+BD)(填“>”,“<”或“=”).