题目内容
17.六棱柱ABCDEF-A1B1C1D1E1F1的底面是正六边形,侧棱垂直于底面,且侧棱长等于底面边长,则直线AE与CB1所成角的余弦值为$\frac{\sqrt{6}}{4}$.分析 由CB1∥EF1,得∠AEF1是异面直线AE与CB1所成角,由此能求出直线AE与CB1所成角的余弦值.
解答 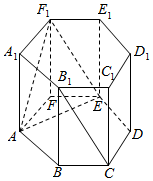 解:∵CB1∥EF1,∴∠AEF1是异面直线AE与CB1所成角,
解:∵CB1∥EF1,∴∠AEF1是异面直线AE与CB1所成角,
设AB=1,则AF1=EF1=$\sqrt{2}$,
AE2=1+1-2×1×1×cos120°=3,即AE=$\sqrt{3}$,
∴cos∠AEF1=$\frac{A{E}^{2}+E{{F}_{1}}^{2}-A{{F}_{1}}^{2}}{2AE•E{F}_{1}}$=$\frac{3+2-2}{2×\sqrt{3}×\sqrt{2}}$=$\frac{\sqrt{6}}{4}$.
∴直线AE与CB1所成角的余弦值为$\frac{\sqrt{6}}{4}$.
故答案为:$\frac{\sqrt{6}}{4}$.
点评 本题考查异面直线所成角的余弦值的求法,是基础题,解题时要认真审题,注意余弦定理的合理运用.

练习册系列答案
相关题目
7.设向量$\overrightarrow{a}$=(1,x),$\overrightarrow{b}$=(x,4),则x=-2是$\overrightarrow{a}$∥$\overrightarrow{b}$的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
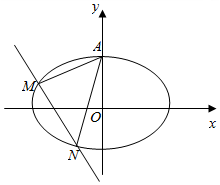 过椭圆$\frac{{x}^{2}}{5}$+$\frac{{y}^{2}}{4}$=1的上顶点A作斜率分别为k1,k2(k1,k2>0,k1≠k2)的两条直线l1,l2,它们分别与椭圆交于另一点M,N.
过椭圆$\frac{{x}^{2}}{5}$+$\frac{{y}^{2}}{4}$=1的上顶点A作斜率分别为k1,k2(k1,k2>0,k1≠k2)的两条直线l1,l2,它们分别与椭圆交于另一点M,N.