题目内容
已知动点M(x,y)到直线l:x=4的距离是它到点N(1,0)的距离的2倍.
(1)求动点M的轨迹C的方程;
(2)过点P(0,3)的直线m与轨迹C交于A,B两点,若A是PB的中点,求直线m的斜率.
解:(1)设M到直线l的距离为d,
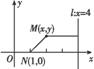
根据题意,d=2|MN|.
由此得|4-x|=2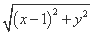 ,
,
化简得 +
+ =1,
=1,
所以,动点M的轨迹方程为 +
+ =1.
=1.
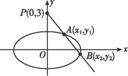
(2)法一 由题意,设直线m的方程为y=kx+3,A(x1,y1),B(x2,y2).
将y=kx+3代入 +
+ =1中,
=1中,
有(3+4k2)x2+24kx+24=0,
其中,Δ=(24k)2-4×24(3+4k2)=96(2k2-3)>0,
由求根公式得,
x1+x2=-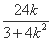 , ①
, ①
x1x2=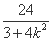 . ②
. ②
又因A是PB的中点,
故x2=2x1,③
将③代入①,②,得
x1=-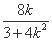 ,
,
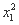 =
=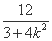 ,
,
可得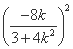 =
=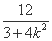 ,
,
且k2> ,
,
解得k=- 或k=
或k= ,
,
所以,直线m的斜率为- 或
或 .
.
法二 由题意,设直线m的方程为y=kx+3,
A(x1,y1),B(x2,y2).
∵A是PB的中点,
∴x1=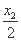 ,①
,①
y1=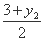 .②
.②
又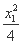 +
+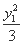 =1,③
=1,③
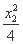 +
+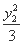 =1.④
=1.④
联立①,②,③,④解得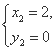 或
或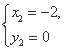
即点B的坐标为(2,0)或(-2,0),
所以,直线m的斜率为- 或
或 .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
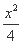 -y2=1的左、右焦点,点P在C上,∠F1PF2=60°,则P到x轴的距离为( )
-y2=1的左、右焦点,点P在C上,∠F1PF2=60°,则P到x轴的距离为( )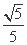 (B)
(B)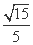 (C)
(C)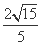 (D)
(D)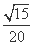
 +
+ =1(a>b>0)的两个焦点,P为椭圆C上一点,且
=1(a>b>0)的两个焦点,P为椭圆C上一点,且 ⊥
⊥ ,若△PF1F2的面积为9,则b= .
,若△PF1F2的面积为9,则b= .  上一点,△F2PF1是底角为30°的等腰三角形,则E的离心率为( )
上一点,△F2PF1是底角为30°的等腰三角形,则E的离心率为( ) (B)
(B) (C)
(C) (D)
(D) 
 a,
a, a)在椭圆上.
a)在椭圆上. +
+ =1上有两个动点P、Q,E(3,0),EP⊥EQ,则
=1上有两个动点P、Q,E(3,0),EP⊥EQ,则 ·
· 的最小值为( )
的最小值为( ) (C)9 (D)12-6
(C)9 (D)12-6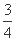 .
. ,直线l:y=kx+
,直线l:y=kx+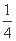 与抛物线C有两个不同的交点A,B,l与圆Q有两个不同的交点D,E,求当
与抛物线C有两个不同的交点A,B,l与圆Q有两个不同的交点D,E,求当 ≤k≤2时,|AB|2+|DE|2的最小值.
≤k≤2时,|AB|2+|DE|2的最小值.