题目内容
正项数列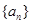 的前n项和为
的前n项和为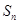 ,且
,且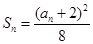 。
。
(Ⅰ)求数列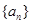 的通项公式
的通项公式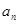 ;
;
(Ⅱ)求证: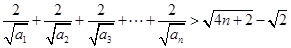 。
。
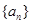 的前n项和为
的前n项和为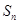 ,且
,且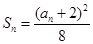 。
。(Ⅰ)求数列
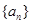 的通项公式
的通项公式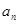 ;
;(Ⅱ)求证:
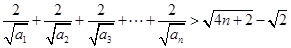 。
。(Ⅰ) ;(Ⅱ)详见解析.
;(Ⅱ)详见解析.
 ;(Ⅱ)详见解析.
;(Ⅱ)详见解析.试题分析:(Ⅰ)求数列
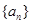 的通项公式
的通项公式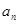 ,由已知
,由已知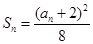 ,这是由
,这是由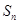 求
求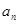 ,可根据
,可根据 来求,因此当
来求,因此当 时,
时, ,解得
,解得 ,当
,当 时,
时, ,整理得
,整理得 ,从而得数列
,从而得数列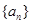 是首项为2,公差为4的等差数列,可写出数列
是首项为2,公差为4的等差数列,可写出数列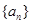 的通项公式;(Ⅱ)求证:
的通项公式;(Ⅱ)求证: ,由(Ⅰ)可知
,由(Ⅰ)可知 ,观察所证问题,显然需对式子变形,但所证问题的形式为
,观察所证问题,显然需对式子变形,但所证问题的形式为 ,这就需要利用放缩法,很容易得证.
,这就需要利用放缩法,很容易得证.试题解析:(Ⅰ)由
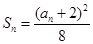 知,当
知,当 时,
时, ,解得
,解得 ;
;当
 时,
时, , (3分)
, (3分)整理得
 ,又
,又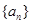 为正项数列,
为正项数列,故
 (
( ),因此数列
),因此数列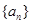 是首项为2,公差为4的等差数列,
是首项为2,公差为4的等差数列, 。(6分)
。(6分)(Ⅱ)由于


=
 (8分)
(8分)因此


=
 。(12分)
。(12分)
练习册系列答案
 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
 (2n
(2n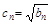 ,
,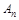 是
是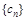 前
前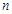 项和,
项和, 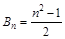 ,当
,当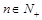 时,试比较
时,试比较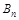 的大小.
的大小. }中,
}中, ,前n项和
,前n项和 .
. ,求数列{
,求数列{ }的前n项和Tn.
}的前n项和Tn.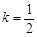 时,数列{an}为递减数列;
时,数列{an}为递减数列;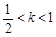 时,数列{an}不一定有最大项;
时,数列{an}不一定有最大项;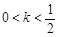 时,数列{an}为递减数列;
时,数列{an}为递减数列;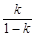 为正整数时,数列{an}必有两项相等的最大项.
为正整数时,数列{an}必有两项相等的最大项.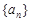 的通项公式
的通项公式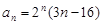 ,则数列
,则数列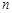 项和
项和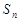 取得最小值时
取得最小值时



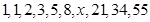 中,
中,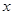 等于( )
等于( )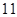



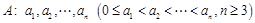 具有性质
具有性质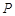 :
: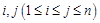 ,
,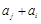 与
与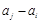 两数中至少有一个是该数列中的一项. 现给出以下四个命题:①数列
两数中至少有一个是该数列中的一项. 现给出以下四个命题:①数列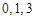 具有性质
具有性质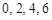 具有性质
具有性质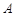 具有性质
具有性质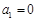 ;
; 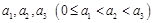 具有性质
具有性质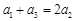 .
. 满足
满足 ,其中
,其中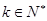 ,设
,设 ,则
,则 等于( ).
等于( ).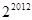
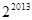


 满足
满足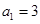 ,
, ,且
,且 ,则
,则