题目内容
设三棱锥P-ABC的顶点P在平面ABC上的射影是H(在△ABC内部),给出以下说法:
①若PA⊥BC,PB⊥AC,则H是△ABC垂心;
②若PA,PB,PC两两互相垂直,则H是△ABC垂心;
③若P到△ABC三边距离等,则H为△ABC的内心;
④若PA=PB=PC,则H是△ABC的外心.
其中正确说法的序号依次是 .
①若PA⊥BC,PB⊥AC,则H是△ABC垂心;
②若PA,PB,PC两两互相垂直,则H是△ABC垂心;
③若P到△ABC三边距离等,则H为△ABC的内心;
④若PA=PB=PC,则H是△ABC的外心.
其中正确说法的序号依次是
考点:棱锥的结构特征
专题:综合题,空间位置关系与距离
分析:根据三角形垂心,外心,内心的定义及棱锥的几何特征,结合勾股定理,逐一判断题目中四个命题的真假,可得答案.
解答:
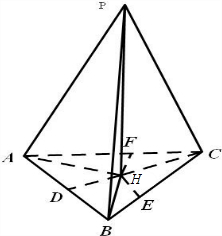 解:①若PA⊥BC,PB⊥AC,因为PH⊥底面ABC,所以AH⊥BC,同理BH⊥AC,可得H是△ABC的垂心,正确.
解:①若PA⊥BC,PB⊥AC,因为PH⊥底面ABC,所以AH⊥BC,同理BH⊥AC,可得H是△ABC的垂心,正确.
②若PA,PB,PC两两互相垂直,容易推出AH⊥BC,同理BH⊥AC,可得H是△ABC的垂心,正确.
③P是△ABC所在平面外一点,若P到△ABC三边的距离相等,E,F,D分别是点P在三个边上的垂足,故可证得HE,HF,HD分别垂直于三边且相等,由内切圆的加心的定义知,此时点H是三角形的内心,故正确
④若PA=PB=PC,易得AH=BH=CH,则H是△ABC的外心,正确.
故答案为:①②③④
 解:①若PA⊥BC,PB⊥AC,因为PH⊥底面ABC,所以AH⊥BC,同理BH⊥AC,可得H是△ABC的垂心,正确.
解:①若PA⊥BC,PB⊥AC,因为PH⊥底面ABC,所以AH⊥BC,同理BH⊥AC,可得H是△ABC的垂心,正确.②若PA,PB,PC两两互相垂直,容易推出AH⊥BC,同理BH⊥AC,可得H是△ABC的垂心,正确.
③P是△ABC所在平面外一点,若P到△ABC三边的距离相等,E,F,D分别是点P在三个边上的垂足,故可证得HE,HF,HD分别垂直于三边且相等,由内切圆的加心的定义知,此时点H是三角形的内心,故正确
④若PA=PB=PC,易得AH=BH=CH,则H是△ABC的外心,正确.
故答案为:①②③④
点评:根据三角形垂心,外心,内心的定义及棱锥的几何特征,结合勾股定理,逐一判断题目中四个命题的真假,可得答案.

练习册系列答案
相关题目
集合A={x|x(3-x)>0},集合B={y|y=2x+2,x∈R},则A∩B=( )
| A、[2,3) |
| B、(2,3) |
| C、(2,+∞) |
| D、(3,+∞) |