题目内容
若棱长均相等的三棱锥叫正四面体，求棱长为a的正四面体的高为 ．
考点：棱锥的结构特征
专题：空间位置关系与距离
分析：设ABCD是棱长为a的正四面体，作AO1⊥平面BCD于O1，则O1为△BCD的中心，求出BO1的长，由此能求出正四面体的高AO1的长．
解答：
解：如图设ABCD是棱长为a的正四面体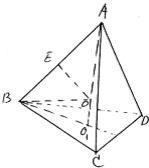
作AO1⊥平面BCD于O1，则O1为△BCD的中心
则BO1=
×
a=
a，
∴正四面体的高为AO1=
=
a，
故答案为：
a．
作AO1⊥平面BCD于O1，则O1为△BCD的中心
则BO1=
| 2 |
| 3 |
| ||
| 2 |
| ||
| 3 |
∴正四面体的高为AO1=
a2-(
|
| ||
| 3 |
故答案为：
| ||
| 3 |
点评：本题考查正四面体的高的求法，是基础题，解题时要熟练掌握正四面体的性质．
练习册系列答案
名校课堂系列答案
相关题目
函数y=a（x+2）+1的图象过定点（ ）
| A、（1，2） |
| B、（2，1） |
| C、（-2，2） |
| D、（-1，1） |