题目内容
8．计算：$\frac{3-i}{1+i}$=1-2i．分析 直接利用复数代数形式的乘除运算化简得答案．
解答 解：$\frac{3-i}{1+i}$=$\frac{（3-i）（1-i）}{（1+i）（1-i）}=\frac{2-4i}{2}=1-2i$，
故答案为：1-2i．
点评 本题考查复数代数形式的乘除运算，是基础的计算题．
练习册系列答案
小学课堂作业系列答案
金博士一点全通系列答案
相关题目
19．
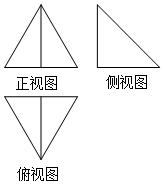一个简单几何体的三视图如图所示，其正视图和俯视图均为正三角形，侧视图为腰长是2的等腰直角三角形则该几何体的体积为（ ）
一个简单几何体的三视图如图所示，其正视图和俯视图均为正三角形，侧视图为腰长是2的等腰直角三角形则该几何体的体积为（ ）| A． | $\frac{4}{9}$$\sqrt{3}$ | B． | 1 | C． | $\frac{8}{9}$$\sqrt{3}$ | D． | 3 |
16．已知$|{\overrightarrow a}|=1$，$|{\overrightarrow b}|=\sqrt{2}$，且$\overrightarrow a⊥（\overrightarrow a+\overrightarrow b）$，则向量$\overrightarrow a$与向量$\overrightarrow b$的夹角为（ ）
| A． | $\frac{π}{6}$ | B． | $\frac{π}{4}$ | C． | $\frac{3π}{4}$ | D． | $\frac{π}{4}$或$\frac{3π}{4}$ |
3．在数列{an}中，已知a3=3，an+1=an+1，前n项的和Sn=55则n为（ ）
| A． | 8 | B． | 9 | C． | 10 | D． | 11 |
13．$|{\frac{1-2i}{2+i}}|$=（ ）
| A． | 1 | B． | $\sqrt{2}$ | C． | -i | D． | 2 |
20．设a=40.1，b=log40.1，c=0.4，则（ ）
| A． | a＞b＞c | B． | b＞a＞c | C． | a＞c＞b | D． | b＞c＞a |
17．复数z=（1+bi）（2+i）是纯虚数，则实数b=（ ）
| A． | -2 | B． | -$\frac{1}{2}$ | C． | $\frac{1}{2}$ | D． | 2 |