题目内容
5.已知函数f(x)=(x-a)2(x-b)(a,b∈R,a<b).(1)当a=1,b=2时,求曲线y=f(x)在点(2,f(2))处的切线方程;
(2)设x1,x2是f(x)的两个极值点,x3是f(x)的一个零点,且x3≠x1,x3≠x2.证明:存在实数x4,使得x1,x2,x3,x4按某种顺序排列后构成等差数列,并求x4.
分析 (1)求出函数的导数,计算f(2),f′(2),求出切线方程即可;(2)求出函数f(x)的极值点,根据等差数列的性质求出x4即可.
解答 解:(1)当a=1,b=2时,因为f′(x)=(x-1)(3x-5),
故f′(2)=1,又f(2)=0,
所以f(x)在点(2,0)处的切线方程为y=x-2.
(2)证明:因为f′(x)=3(x-a)(x-$\frac{a+2b}{3}$),
由于a<b,故a<$\frac{a+2b}{3}$,
所以f(x)的两个极值点为x=a或x=$\frac{a+2b}{3}$,
不妨设x1=a,x2=$\frac{a+2b}{3}$,
因为x3≠x1,x3≠x2,且x3是f(x)的零点,故x3=b,
又因为$\frac{a+2b}{3}$-a=2(b-$\frac{a+2b}{3}$),x4=$\frac{1}{2}$(a+$\frac{a+2b}{3}$)=$\frac{2a+b}{3}$,
此时a,$\frac{2a+b}{3}$,$\frac{a+2b}{3}$,b依次成等差数列,
所以存在实数x4满足题意,且x4=$\frac{2a+b}{3}$.
点评 本题考查了切线方程问题,考查导数的应用以及等差数列的性质,是一道中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
17.在△ABC中,角A,B,C所对的边分别为a,b,c,已知cosA=$\frac{1}{3}$.求sin(B+C)的值( )
| A. | $\frac{{2\sqrt{2}}}{3}$ | B. | -$\frac{1}{2}$ | C. | 0 | D. | $\frac{3}{4}$ |
15.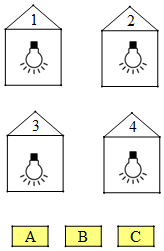 如图,A,B,C三个开关控制着1,2,3,4号四盏灯.若开关A控制着2,3,4号灯(即按一下开关A,2,3,4号灯亮,再按一下开关A,2,3,4号灯熄灭),同样,开关B控制着1,3,4号灯,开关C控制着1,2,4号灯.开始时,四盏灯都亮着,那么下列说法正确的是( )
如图,A,B,C三个开关控制着1,2,3,4号四盏灯.若开关A控制着2,3,4号灯(即按一下开关A,2,3,4号灯亮,再按一下开关A,2,3,4号灯熄灭),同样,开关B控制着1,3,4号灯,开关C控制着1,2,4号灯.开始时,四盏灯都亮着,那么下列说法正确的是( )
 如图,A,B,C三个开关控制着1,2,3,4号四盏灯.若开关A控制着2,3,4号灯(即按一下开关A,2,3,4号灯亮,再按一下开关A,2,3,4号灯熄灭),同样,开关B控制着1,3,4号灯,开关C控制着1,2,4号灯.开始时,四盏灯都亮着,那么下列说法正确的是( )
如图,A,B,C三个开关控制着1,2,3,4号四盏灯.若开关A控制着2,3,4号灯(即按一下开关A,2,3,4号灯亮,再按一下开关A,2,3,4号灯熄灭),同样,开关B控制着1,3,4号灯,开关C控制着1,2,4号灯.开始时,四盏灯都亮着,那么下列说法正确的是( )| A. | 只需要按开关A,C可以将四盏灯全部熄灭 | |
| B. | 只需要按开关B,C可以将四盏灯全部熄灭 | |
| C. | 按开关A,B,C可以将四盏灯全部熄灭 | |
| D. | 按开关A,B,C无法将四盏灯全部熄灭 |