题目内容
20.求过直线l1:x-y+4=0与l2:2x+y+5=0的交点,倾斜角为45°的直线方程.分析 解方程组可得直线的交点,求正切值可得直线的斜率,可得直线的方程.
解答 解:解方程组$\left\{\begin{array}{l}{x-y+4=0}\\{2x+y+5=0}\end{array}\right.$可得$\left\{\begin{array}{l}{x=-3}\\{y=1}\end{array}\right.$,
故直线l1与l2的交点为(-3,1),
再由倾斜角为45°可得直线的斜率为tan45°=1,
∴所求直线的方程为y-1=x+3,即x-y+4=0
点评 本题考查直线的方程的求解,涉及直线的交点和斜率,属基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
15.设函数f(x)=|x+a|(|x-a+1|+|x-3|+2)的图象是轴对称图形,则实数a的值为( )
| A. | -$\frac{2}{3}$ | B. | $\frac{2}{3}$ | C. | -1 | D. | 2 |
10.函数f(x)=$\sqrt{4{x}^{2}+4x+2}$+$\sqrt{4{x}^{2}-12x+13}$的值域是( )
| A. | [3,+∞) | B. | [5,+∞) | C. | [$\sqrt{2}$+$\sqrt{13}$,+∞) | D. | [6,+∞) |
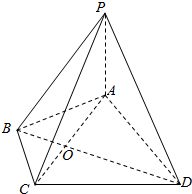 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,AB=BC=2,∠ABD=∠CBD=60°.
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,AB=BC=2,∠ABD=∠CBD=60°.