题目内容
已知数列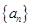 满足:
满足: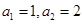 ,且
,且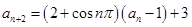 ,
,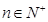 .
.
(1)求通项公式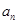 ;
;
(2)求数列的前n项的和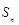
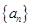 满足:
满足: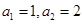 ,且
,且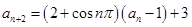 ,
,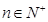 .
.(1)求通项公式
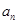 ;
;(2)求数列的前n项的和
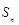
(1) ;(2)
;(2) .
.
 ;(2)
;(2) .
.试题分析:(1)求通项公式
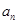 由已知
由已知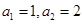 ,且
,且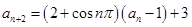 ,
,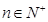 ,由于
,由于 取奇数,与
取奇数,与 取偶数影响解析式,因此需对
取偶数影响解析式,因此需对 讨论,当
讨论,当 是奇数时,
是奇数时, ,得
,得 ,
,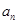 故数列
故数列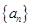 的奇数项
的奇数项 是等差数列,可求出通项公式,当
是等差数列,可求出通项公式,当 为偶数时,
为偶数时, ,则
,则 ,数列
,数列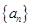 的偶数项
的偶数项 是等比数列,可求出通项公式,从而可得数列
是等比数列,可求出通项公式,从而可得数列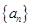 的通项公式
的通项公式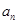 ;(2)求数列的前
;(2)求数列的前 项的和
项的和 ,由(1)知数列
,由(1)知数列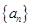 的通项公式
的通项公式 ,故它的前
,故它的前 项的和
项的和 分情况求.
分情况求.试题解析:(1)当
 是奇数时,
是奇数时, ,所以
,所以 ,所以
,所以 是首项为
是首项为 ,公差为2的等差数列,因此
,公差为2的等差数列,因此 。 2分
。 2分当
 为偶数时,
为偶数时, ,所以
,所以 ,所以
,所以 是首项为
是首项为 ,公比为3的等比数列,因此
,公比为3的等比数列,因此 。 4分
。 4分综上
 6分
6分(2)由(1)得
 8分
8分 10分
10分所以
 12分
12分 项的和.
项的和.
练习册系列答案
 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
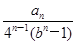 ,证明:c1+c2+c3+…+cn<3.
,证明:c1+c2+c3+…+cn<3. ,n∈N*,则S1+S2+S3+…+S100=________.
,n∈N*,则S1+S2+S3+…+S100=________.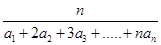 为{an}的“光阴”值,现知某数列的“光阴”值为Hn=
为{an}的“光阴”值,现知某数列的“光阴”值为Hn=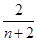 ,则数列{an}的通项公式为________.
,则数列{an}的通项公式为________.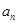 }为等差数列,若
}为等差数列,若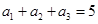 ,
,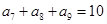 ,则
,则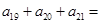 ________.
________.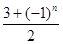 ,数列{an}满足an=d1+d2+d3+…+d2n,又知在数列{bn}中,b1=2,且对任意正整数m,n,
,数列{an}满足an=d1+d2+d3+…+d2n,又知在数列{bn}中,b1=2,且对任意正整数m,n,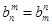 .
. ,则tan (a4+a6)=( ).
,则tan (a4+a6)=( ).

 中,各项都是正数,且
中,各项都是正数,且 成等差数列,则
成等差数列,则 ( )
( )


