题目内容
9.已知α是第三象限角,且f(α)=$\frac{sin(α-\frac{π}{2})cos(\frac{3π}{2}+α)tan(π-α)}{tan(-α-π)sin(-π-α)}$.(1)化简f(α);
(2)若cos(α-$\frac{3}{2}$π)=$\frac{1}{5}$,求f(α)的值.
分析 (1)利用诱导公式化解可得f(α);
(2)根据同角三角函数关系式和诱导公式化简即可求值.
解答 解:(1)由f(α)=$\frac{sin(α-\frac{π}{2})cos(\frac{3π}{2}+α)tan(π-α)}{tan(-α-π)sin(-π-α)}$=$\frac{-cosαsinα•(-tanα)}{-tanαsinα}$=-cosα.
(2)∵cos(α-$\frac{3}{2}$π)=$\frac{1}{5}$,
∴-sinα=$\frac{1}{5}$,即sinα=-$\frac{1}{5}$,
∵α是第三象限角
∴cosα=-$\frac{2\sqrt{6}}{5}$,
由(1)得:f(α)=-cosα=$\frac{2\sqrt{6}}{5}$.
点评 本题主要考察了同角三角函数关系式和诱导公式的应用,属于基本知识的考查.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
6.将函数$y=sin(2x+\frac{π}{6})$的图象向左平移m(m>0)个单位长度,得到函数y=f(x)图象在区间$[-\frac{π}{12},\frac{5π}{12}]$上单调递减,则m的最小值为( )
| A. | $\frac{π}{12}$ | B. | $\frac{π}{6}$ | C. | $\frac{π}{4}$ | D. | $\frac{π}{3}$ |
4.sin20°sin10°-cos10°sin70°=( )
| A. | $\frac{\sqrt{3}}{2}$ | B. | -$\frac{\sqrt{3}}{2}$ | C. | $\frac{1}{2}$ | D. | -$\frac{1}{2}$ |
1.若变量x,y满足约束条件$\left\{\begin{array}{l}x+2y≤2\\ x+y≥0\\ x≤4\end{array}\right.$,则z=2x+y的最大值为( )
| A. | 2 | B. | 8 | C. | 5 | D. | 7 |
18.已知函数f(x)的定义域为[-2,2],且f(x)在[-2,2]上是增函数,f(1-m)<f(m),则实数m的取值范围为( )
| A. | $(\frac{1}{2},+∞)$ | B. | $(-∞,\frac{1}{2})$ | C. | $({\frac{1}{2},2}]$ | D. | $[{-2,\frac{1}{2}})$ |
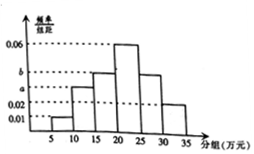 某统计部门就“A市汽车价格区间的购买意愿”对100人进行了问卷调查,并将结果制作成频率分布直方图,如图,已知样本中数据在区间[10,15)上的人数与数据在区间[25,30)的人数之比为3:4.
某统计部门就“A市汽车价格区间的购买意愿”对100人进行了问卷调查,并将结果制作成频率分布直方图,如图,已知样本中数据在区间[10,15)上的人数与数据在区间[25,30)的人数之比为3:4.