题目内容
3.已知△ABC的三边长是a,b,c,且m为正数,求证:$\frac{a}{a+m}$+$\frac{b}{b+m}$>$\frac{c}{c+m}$.分析 利用a+b>c、$\frac{a}{a+m}$>$\frac{a}{a+b+m}$、$\frac{b}{b+m}$>$\frac{b}{a+b+m}$放缩、相加即得结论.
解答 证明:依题意,a、b、c、m均大于0且a+b>c,
∴$\frac{a}{a+m}$+$\frac{b}{b+m}$>$\frac{a}{a+b+m}$+$\frac{b}{a+b+m}$
=$\frac{a+b}{a+b+m}$
>$\frac{c}{c+m}$,
即$\frac{a}{a+m}$+$\frac{b}{b+m}$>$\frac{c}{c+m}$.
点评 本题考查不等式的证明,利用不等式的性质进行放缩是解决本题的关键,注意解题方法的积累,属于基础题.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
12.已知a=log3$\frac{1}{4}$,b=3${\;}^{-\frac{1}{3}}$,c=log${\;}_{\frac{1}{2}}$2,则( )
| A. | a<b<c | B. | b<c<a | C. | a<c<b | D. | c<a<b |
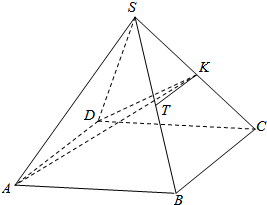 如图,正四棱锥S-ABCD中,底面边长与高相等,K、T分别是SC、SB的中点.
如图,正四棱锥S-ABCD中,底面边长与高相等,K、T分别是SC、SB的中点. 如图,△ABC为等腰直角三角形,∠ACB=90°,PA⊥面ABC,AC=a,PA=$\sqrt{2}$a.
如图,△ABC为等腰直角三角形,∠ACB=90°,PA⊥面ABC,AC=a,PA=$\sqrt{2}$a.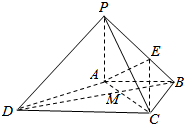 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,AB∥DC,AB⊥BC,且PA=AB=BC=$\frac{1}{2}$CD,BE=$\frac{1}{3}$BP.
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,AB∥DC,AB⊥BC,且PA=AB=BC=$\frac{1}{2}$CD,BE=$\frac{1}{3}$BP.