题目内容
18.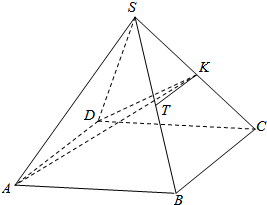 如图,正四棱锥S-ABCD中,底面边长与高相等,K、T分别是SC、SB的中点.
如图,正四棱锥S-ABCD中,底面边长与高相等,K、T分别是SC、SB的中点.(1)求证:KT∥平面SAD;
(2)求二面角K-AD-C的余弦值.
分析 (1)由已知利用平行公理得到KT∥AD,由此能证明KT∥平面SAD.
(2)过点K在面KAD内作KE⊥AD,交AD于E,过点E作EF∥AB交BC于F,连接KF,∠KEF为二面角K-AD-C的平面角,由此能求出二面角K-AD-C的余弦值.
解答 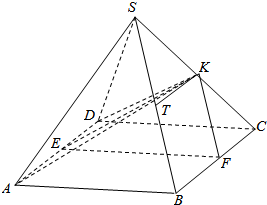 (1)证明:∵正四棱锥S-ABCD中,底面边长与高相等,K、T分别是SC、SB的中点,
(1)证明:∵正四棱锥S-ABCD中,底面边长与高相等,K、T分别是SC、SB的中点,
∴KT∥BC,AD∥BC,∴KT∥AD,
∵AD?平面SAD,KT?平面SAD,
∴KT∥平面SAD.
(2)解:过点K在面KAD内作KE⊥AD,交AD于E,过点E作EF∥AB交BC于F,连接KF,
∵正四棱锥S-ABCD中,底面边长与高相等,K是SC的中点,
∴KD=KA,∴E⊥AD,∵AB⊥AD,EF∥AB,∴EF⊥AD,
则∠KEF为二面角K-AD-C的平面角,
设正四棱锥S-ABCD菱长为a,
则KD=KA=$\sqrt{{a}^{2}-(\frac{1}{2}a)^{2}}$=$\frac{\sqrt{3}}{2}a$,KE=$\sqrt{(\frac{\sqrt{3}}{2}a)^{2}-(\frac{1}{2}a)^{2}}$=$\frac{\sqrt{2}}{2}a$,EF=a,KF=KC=FC=$\frac{1}{2}a$,
∴cos∠KEF=$\frac{(\frac{\sqrt{2}}{2}a)^{2}+{a}^{2}-(\frac{1}{2}a)^{2}}{2×\frac{\sqrt{2}}{2}a×a}$=$\frac{5\sqrt{2}}{8}$.
∴二面角K-AD-C的余弦值为$\frac{5\sqrt{2}}{8}$.
点评 本题考查线面平行的证明,考查二面角的余弦值的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.

 名校课堂系列答案
名校课堂系列答案| A. | (1,+∞) | B. | (-∞,1)∪(2,+∞) | C. | (0,1) | D. | (-∞,0)∪(0,+∞) |
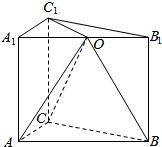 如图,在三棱柱ABC-A1B1C1中,点C在平面A1B1C1内的射影点为A1B1的中点O,且AC:BC:AB:AA1=1:1:$\sqrt{2}$:2.
如图,在三棱柱ABC-A1B1C1中,点C在平面A1B1C1内的射影点为A1B1的中点O,且AC:BC:AB:AA1=1:1:$\sqrt{2}$:2.