题目内容
15.已知m、n∈N*,求证:$\sqrt{mn(m+2)(n+2)}$-$\sqrt{mn(mn+2)}$≥3-$\sqrt{3}$.分析 会发现,m=n=1时,要证的不等式的等号成立,从而可考虑用函数的单调性来证明:先根据基本不等式,$(m+2)(n+2)=mn+2(m+n)+4≥mn+4\sqrt{mn}+4$,从而得到$\sqrt{(m+2)(n+2)}-\sqrt{mn+2}$$≥\sqrt{mn+4\sqrt{mn}+4}-\sqrt{mn+2}$,这样可令$\sqrt{mn}=t$,t≥1.从而可以得到$\sqrt{mn+4\sqrt{mn}+4}-\sqrt{mn+2}=t+2-\sqrt{{t}^{2}+2}$,可设$f(t)=t+2-\sqrt{{t}^{2}+2}$,然后可通过求导数,判断出函数f(t)在[1,+∞)上单调递增,这样便可得出f(t)$≥3-\sqrt{3}$,这样便可得出要证明的不等式成立.
解答 解:(m+2)(n+2)=mn+2(m+n)+4≥mn$+4\sqrt{mn}+4$,m=n时取“=”;
∴$\sqrt{(m+2)(n+2)}-\sqrt{mn+2}$$≥\sqrt{mn+4\sqrt{mn}+4}-\sqrt{mn+2}$,令$\sqrt{mn}=t$,t≥1;
∴$\sqrt{mm+4\sqrt{mn}+4}-\sqrt{mn+2}$=$\sqrt{mn}+2-\sqrt{mn+2}=t+2-\sqrt{{t}^{2}+2}$,设$f(t)=t+2-\sqrt{{t}^{2}+2},t≥1$;
∴$f′(t)=1-\frac{t}{\sqrt{{t}^{2}+2}}$;
$t<\sqrt{{t}^{2}+2}$;
∴$\frac{t}{\sqrt{{t}^{2}+2}}<1$;
∴f′(t)>0;
∴f(t)在[1,+∞)上单调递增;
∴$f(t)≥f(1)=3-\sqrt{3}$;
∴$\sqrt{mn+4\sqrt{mn}+4}-\sqrt{mn+2}≥3-\sqrt{3}$,m=n=1时取“=”;
∴$\sqrt{(m+2)(n+2)}-\sqrt{mn+2}≥3-\sqrt{3}$,m=n=1时取“=”;
∴$\sqrt{mn(m+2)(n+2)}-\sqrt{mn(mn+2)}$$≥(3-\sqrt{3})mn≥3-\sqrt{3}$,当m=n=1时取“=”;
即$\sqrt{mn(m+2)(n+2)}-\sqrt{mn(mn+2)}≥3-\sqrt{3}$.
点评 考查构造函数解决问题的方法,基本不等式的应用,根据导数符号判断函数单调性的方法,以及函数单调性定义的运用,不等式的性质.

| A. | (1,+∞) | B. | (-∞,1)∪(2,+∞) | C. | (0,1) | D. | (-∞,0)∪(0,+∞) |
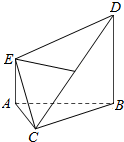 在四棱锥C-ABDE中,F为CD的中点,DB⊥平面ABC,AE∥BD,AB=BC=CA=BD=2AE.
在四棱锥C-ABDE中,F为CD的中点,DB⊥平面ABC,AE∥BD,AB=BC=CA=BD=2AE.