题目内容
12.已知x,y满足$\left\{\begin{array}{l}x+2y-3≤0\\ x+3y-3≥0\\ y≤1\end{array}\right.$,z=2x+y的最大值为m,若正数a,b满足a+b=m,则$\frac{1}{a}+\frac{4}{b}$的最小值为( )| A. | 3 | B. | $\frac{3}{2}$ | C. | 2 | D. | $\frac{5}{2}$ |
分析 作出不等式组对应的平面区域,利用目标函数的几何意义,求最大值m,然后根据基本不等式的性质进行求解即可.
解答 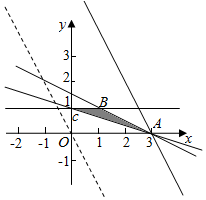 解:作出不等式组对应的平面区域如图:(阴影部分)
解:作出不等式组对应的平面区域如图:(阴影部分)
由z=2x+y得y=-2x+z,平移直线y=-2x+z,
由图象可知当直线y=-2x+z经过点A(3,0)时,直线y=-2x+z的截距最大,此时z最大.
代入目标函数z=2x+y得z=2×3=6.
即m=6.
则a+b=6,即$\frac{a}{6}$+$\frac{b}{6}$=1,
则$\frac{1}{a}+\frac{4}{b}$=($\frac{1}{a}+\frac{4}{b}$)($\frac{a}{6}$+$\frac{b}{6}$)=$\frac{1}{6}$+$\frac{4}{6}$+$\frac{4a}{6b}$+$\frac{b}{6a}$≥$\frac{5}{6}$+2$\sqrt{\frac{4a}{6b}•\frac{b}{6a}}$=$\frac{5}{6}$+2×$\frac{2}{6}$=$\frac{3}{2}$,当且仅当$\frac{4a}{6b}$=$\frac{b}{6a}$,即b=2a时取等号,
故选:B.
点评 本题主要考查线性规划以及基本不等式的应用,利用目标函数的几何意义,结合数形结合的数学思想是解决此类问题的基本方法.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
2.若x,y满足约束条件$\left\{\begin{array}{l}x-y+1≥0\\ x-2y≤0\\ x+2y-2≤0\end{array}\right.$,则z=2x-y的最大值为( )
| A. | $\frac{3}{2}$ | B. | -1 | C. | 2 | D. | -3 |
3.阅读如图的程序框图,运行相应的程序,则输出S的值为( )


| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
20.命题p:?x0∈R,不等式$cos{x_0}+{e^{x_0}}-1<0$成立,则p的否定为( )
| A. | ?x0∈R,不等式$cos{x_0}+{e^{x_0}}-1≥0$成立 | |
| B. | ?x∈R,不等式cosx+ex-1<0成立 | |
| C. | ?x∈R,不等式cosx+ex-1≥0成立 | |
| D. | ?x∈R,不等式cosx+ex-1>0成立 |
17.已知复数z1、z2在复平面内对应的点分别为A(1,-1)、B(3,1),则$\frac{z_2}{z_1}$=( )
| A. | 1+2i | B. | 2+i | C. | 1+3i | D. | 3+i |
2.若x>0,且x≠1,则函数y=lgx+logx10的值域为( )
| A. | R | B. | [2,+∞) | C. | (-∞,-2] | D. | (-∞,-2]∪[2,+∞) |