题目内容
下列函数中，以π为最小正周期的偶函数，且在（
，π）上为减函数的是（ ）
| π |
| 2 |
| A、y=sin2x+cos2x |
| B、y=|sinx| |
| C、y=cos2x |
| D、y=tanx |
考点：三角函数的周期性及其求法,正弦函数的单调性
专题：三角函数的图像与性质
分析：分别根据函数的单调性奇偶性和周期性进行判定即可得到结论．
解答：
解：A、函数y=sin2x+cos2x=
six（2x+
）的最小正周期为π，非奇非偶函数．
B、y=|sinx|是偶函数，在（
，π）内递减，周期为π，是周期函数．满足条件．
C、y=cos2x=
cos2x+
在（
，π）内先递减后递增，不满足条件；
D、，函数y=tanx为奇函数，不满足条件；
故选：B．
| 2 |
| π |
| 4 |
B、y=|sinx|是偶函数，在（
| π |
| 2 |
C、y=cos2x=
| 1 |
| 2 |
| 1 |
| 2 |
| π |
| 2 |
D、，函数y=tanx为奇函数，不满足条件；
故选：B．
点评：本题主要考查三角函数的图象和性质，要求熟练掌握三角函数的周期性，单调性和奇偶性的性质，属于基本知识的考查．
练习册系列答案
举一反三单元同步过关卷系列答案
相关题目
已知函数f（x），g（x），F（x）的定义域都为R，且在定义域内f（x）为增函数，g（x）为减函数，F（x）=mf（x）+ng（x）（m，n为常数，F（x）不是常函数），在下列哪种情况下，F（x）在定义域内一定是单调函数（ ）
| A、m+n＞0 | B、m+n＜0 |
| C、mn＞0 | D、mn＜0 |
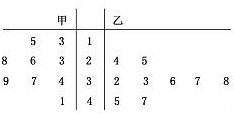2014年的NBA全明星塞于美国当地时间2014年2月17日在新奥尔良市举行．如图是参加此次比赛的甲、乙两名篮球运动员以往几场比赛得分的茎叶图，则甲、乙两人这几场比赛得分的中位数之和是（ ）| A、59 | B、64 | C、62 | D、67 |
在△ABC中，若a=3，cosA=-
，则△ABC的外接圆半径是（ ）
| 1 |
| 2 |
A、
| ||||
B、
| ||||
C、2
| ||||
D、
|
不等式
≤x-2的解集是（ ）
| 4 |
| x-2 |
| A、（-∞，0）∪（2，4） |
| B、[0，2）∪[4，+∞） |
| C、[2，4] |
| D、（-∞，2]∪（4，+∞） |
若直线x+ay-1=0和直线（a+1）x+3y=0垂直，则a等于（ ）
A、
| ||
B、-
| ||
C、
| ||
D、-
|