题目内容
已知
,
是空间中两个相互垂直的单位向量,且|
|=3,
•
=1,
•
=2,则对于任意实数t1,t2,|
-t1
-t2
|的最小值是( )
| a |
| b |
| c |
| c |
| a |
| c |
| b |
| c |
| a |
| b |
A、
| ||
B、
| ||
| C、2 | ||
| D、4 |
考点:平面向量数量积的运算
专题:平面向量及应用
分析:根据题意,(
)2=(
)2=1,且
•
=0,将此代入|
-t1
-t2
|的式子,并且结合|
|=3,
•
=1,
•
=2,化简整理得到关于实数t1,t2的方程,当且仅当t1=1,t2=2时,|
-t1
-t2
|2的最小值为4,
| a |
| b |
| a |
| b |
| c |
| a |
| b |
| c |
| c |
| a |
| c |
| b |
| c |
| a |
| b |
解答:
解:|
-t1
-t2
|2=(
)2+t12(
)2+t22(
)2-2t1(
•
)-2t2(
•
)+2t1t2(
•
)
∵
,
是空间中两个相互垂直的单位向量,且|
|=3,
•
=1,
•
=2,
∴|
-t1
-t2
|2=9+t12+t22-2t1-4t2=(t1-1)2+(t2-2)2+4,
由此可得,当且仅当t1=1,t2=2时,|
-t1
-t2
|2的最小值为4,
∴|
-t1
-t2
|的最小值是
=2.
故选:C.
| c |
| a |
| b |
| c |
| a |
| b |
| c |
| a |
| c |
| b |
| a |
| b |
∵
| a |
| b |
| c |
| c |
| a |
| c |
| b |
∴|
| c |
| a |
| b |
由此可得,当且仅当t1=1,t2=2时,|
| c |
| a |
| b |
∴|
| c |
| a |
| b |
| 4 |
故选:C.
点评:本题主要考查了平面向量的数量积及其运算性质和二次式的最值等知识,属于中档题.

练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
若变量x,y满足约束条件
,则2x+y的最大值是( )
|
| A、2 | B、4 | C、7 | D、8 |
抛物线y=
x2的准线方程是( )
| 1 |
| 4 |
| A、y=-1 | B、y=-2 |
| C、x=-1 | D、x=-2 |
已知F为双曲线C:x2-my2=3m(m>0)的一个焦点,则点F到C的一条渐近线的距离为( )
A、
| ||
| B、3 | ||
C、
| ||
| D、3m |
已知向量
=(k,3),
=(1,4),
=(2,1)且(2
-3
)⊥
,则实数k=( )
| a |
| b |
| c |
| a |
| b |
| c |
A、-
| ||
| B、0 | ||
| C、3 | ||
D、
|
下列叙述中正确的是( )
| A、若a,b,c∈R,则“ax2+bx+c≥0”的充分条件是“b2-4ac≤0” |
| B、若a,b,c∈R,则“ab2>cb2”的充要条件是“a>c” |
| C、命题“对任意x∈R,有x2≥0”的否定是“存在x∈R,有x2≥0” |
| D、l是一条直线,α,β是两个不同的平面,若l⊥α,l⊥β,则α∥β |
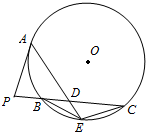 如图,P是⊙O外一点,PA是切线,A为切点,割线PBC与⊙O相交于点B,C,PC=2PA,D为PC的中点,AD的延长线交⊙O于点E,证明:
如图,P是⊙O外一点,PA是切线,A为切点,割线PBC与⊙O相交于点B,C,PC=2PA,D为PC的中点,AD的延长线交⊙O于点E,证明: