题目内容
已知λ为非零常数，数列{an}与{2an+λ}均为等比数列，且a2012=3，则a1= ．
考点：等比数列的通项公式
专题：等差数列与等比数列
分析：设出等比数列{an}的公比，由{2an+λ}为等比数列得到（1-q）λ=0，求出数列{an}的公比为1，则答案可求．
解答：
解：设{an}的公比为q，由{2an+λ}为等比数列，得
=
=
=q+
．
要使{2an+λ}为等比数列，则q+
是常数，
∴（1-q）λ=0，
∵λ≠0，因此只有1-q=0，q=1．
∴数列{an}是以1为公比的等比数列，也是各项均为3的常数数列．
则a1=a2012=3．
故答案为：3．
| 2an+1+λ |
| 2an+λ |
| 2an•q+λ |
| 2an+λ |
| 2an•q+qλ+(1-q)λ |
| 2an+λ |
=q+
| (1-q)λ |
| 2a1qn-1+λ |
要使{2an+λ}为等比数列，则q+
| (1-q)λ |
| 2a1qn-1+λ |
∴（1-q）λ=0，
∵λ≠0，因此只有1-q=0，q=1．
∴数列{an}是以1为公比的等比数列，也是各项均为3的常数数列．
则a1=a2012=3．
故答案为：3．
点评：本题考查了等比数列的通项公式，考查了等比关系的确定，体现了数列的函数特性，是中档题．
练习册系列答案
相关题目
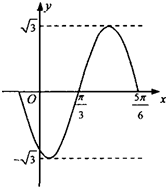已知函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，-π＜φ＜π）的部分图象如图所示，为了得到g（x）=| 3 |
A、向左平移
| ||
B、向左平移
| ||
C、向右平移
| ||
D、向右平移
|
如果lgx+lgx2+…+lgx10=110，那么lgx+lg2x+…+lg10x=（ ）
| A、211-2 |
| B、211+2 |
| C、210+2 |
| D、210-2 |