题目内容
如图,在四棱锥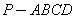 中,
中,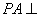 底面
底面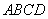 ,
,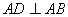 ,
, 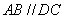 ,
, 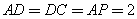 ,
,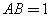 ,点
,点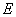 为棱
为棱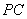 的中点.
的中点.
(1)证明 ;
;
(2)若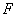 为棱
为棱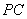 上一点,满足
上一点,满足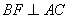 ,求二面角
,求二面角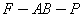 的余弦值.
的余弦值.
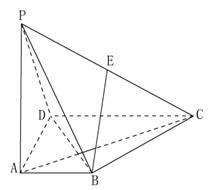
依题意,以点 为原点建立空间直角坐标系,
为原点建立空间直角坐标系,
可得 ,
, ,
, ,
, .由
.由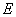 为棱
为棱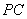 的中点,得
的中点,得 .
.
(1)向量 ,
, ,故
,故 . 所以,
. 所以, .
.
(2)向量 ,
, ,
,  ,
, .
.
由点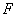 在棱
在棱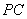 上,设
上,设 ,
, .
.
故 .
.
由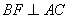 ,得
,得 ,
,
因此, ,解得
,解得 .
.
即 .
.
设 为平面
为平面 的法向量,则
的法向量,则 即
即
不妨令 ,可得
,可得 为平面
为平面 的一个法向量.
的一个法向量.
取平面 的法向量
的法向量 ,则
,则
 .
.
易知,二面角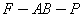 是锐角,所以其余弦值为
是锐角,所以其余弦值为 .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

 , (1)求逆矩阵
, (1)求逆矩阵 错误!未找到引用源。;(2)若矩阵
错误!未找到引用源。;(2)若矩阵 满足
满足 ,试求矩阵
,试求矩阵 中,内角
中,内角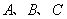 所对的边分别为
所对的边分别为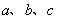 ,
,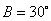 ,
,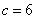 ,令
,令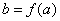 .
.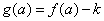 (
(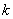 是常数)只有一个零点.则实数
是常数)只有一个零点.则实数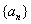 的各项均为正数,若对任意的
的各项均为正数,若对任意的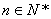 ,存在
,存在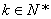 ,
,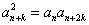 成立,则称数列
成立,则称数列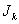 型”数列.
型”数列.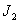 型”数列,且
型”数列,且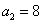 ,
,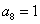 ,求
,求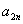 ;
;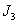 型”数列,又是“
型”数列,又是“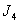 型”数列,证明数列
型”数列,证明数列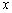 的值为1,则输出
的值为1,则输出 的值为 .
的值为 .
 ,
, 是棱
是棱 的中点,
的中点, 是线段
是线段 上的
上的 与△
与△ 的面积和的最小值是 .
的面积和的最小值是 . 的最小正周期为
的最小正周期为 ,其中
,其中 ,则
,则 .
.