题目内容
设数列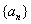 的各项均为正数,若对任意的
的各项均为正数,若对任意的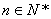 ,存在
,存在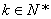 ,
,
使得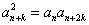 成立,则称数列
成立,则称数列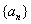 为“
为“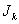 型”数列.
型”数列.
(1)若数列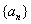 是“
是“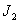 型”数列,且
型”数列,且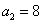 ,
,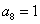 ,求
,求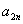 ;
;
(2)若数列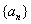 既是“
既是“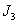 型”数列,又是“
型”数列,又是“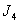 型”数列,证明数列
型”数列,证明数列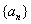 是等比数列.
是等比数列.
(1)由题意得, 成等比数列,且公比
成等比数列,且公比 ,
,
 .
.
(2)由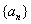 是“
是“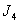 型”数列得
型”数列得 …成等比数列,设公比为
…成等比数列,设公比为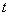 .
.
由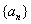 是“
是“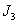 型”数列得
型”数列得 …成等比数列,设公比为
…成等比数列,设公比为 ;
;
 …成等比数列,设公比为
…成等比数列,设公比为 ;
;
 …成等比数列,设公比为
…成等比数列,设公比为 ;
;
则 ,
, ,
, ,
,
 ,不妨令
,不妨令 ,则
,则 .
.


 ,
,
综上, ,从而
,从而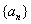 是等比数列.
是等比数列.

练习册系列答案
 每课必练系列答案
每课必练系列答案
相关题目
 ,其中
,其中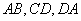 都是线段,曲线段
都是线段,曲线段 是抛物线的一部分,且点
是抛物线的一部分,且点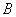 是该抛物线的顶点,
是该抛物线的顶点,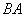 所在直线是该抛物线的对称轴. 经测量,
所在直线是该抛物线的对称轴. 经测量,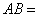 2米,
2米,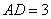 米,
米,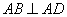 ,点
,点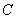 到
到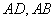 的距离
的距离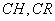 的长均为1米.现要用这块边角料裁一个矩形
的长均为1米.现要用这块边角料裁一个矩形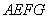 (其中点
(其中点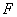 在曲线段
在曲线段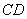 上,点
上,点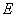 在线段
在线段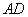 上,点
上,点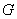 在线段
在线段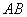 上). 设
上). 设 的长为
的长为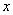 米,矩形
米,矩形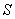 平方米.
平方米.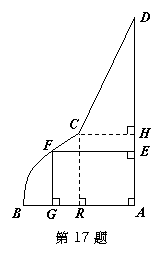
 是定义域为
是定义域为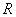 的奇函数,对于任意的
的奇函数,对于任意的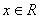
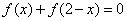 ,则函数
,则函数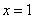 对称;
对称;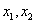 是函数
是函数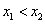 时,
时,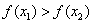 ,则
,则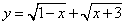 的最大值和最小值分别为
的最大值和最小值分别为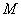 和
和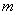 ,则
,则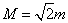 ;
;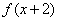 也为奇函数,则
也为奇函数,则 中,角
中,角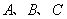 的对边分别为
的对边分别为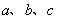 ,已知
,已知 ,
, 的值;
的值; ,求
,求 的值.
的值.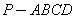 中,
中,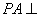 底面
底面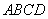 ,
,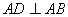 ,
, 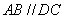 ,
, 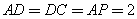 ,
,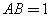 ,点
,点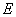 为棱
为棱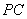 的中点.
的中点.  ;
;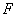 为棱
为棱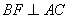 ,求二面角
,求二面角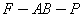 的余弦值.
的余弦值.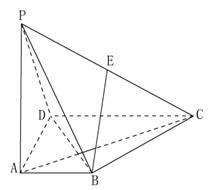
 为边,
为边, 为对角线的矩形中,
为对角线的矩形中, ,
, ,则实数
,则实数 .
.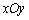 中,椭圆
中,椭圆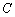 的参数方程为
的参数方程为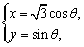 其中
其中 为参数.以
为参数.以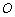 为
为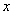 轴正半轴为极轴建立极坐标系,直线l的极坐标方程为
轴正半轴为极轴建立极坐标系,直线l的极坐标方程为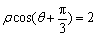 .求
.求
 B.
B. 


