题目内容
4.已知$tanα=\frac{1}{2}$,则sin2α的值为$\frac{4}{5}$.分析 利用同角三角函数的基本关系,二倍角的正弦公式,求得sin2α的值.
解答 解:∵已知$tanα=\frac{1}{2}$,则sin2α=$\frac{2sinαcosα}{{sin}^{2}α{+cos}^{2}α}$=$\frac{2tanα}{1{+tan}^{2}α}$=$\frac{1}{1+\frac{1}{4}}$=$\frac{4}{5}$,
故答案为:$\frac{4}{5}$.
点评 本题主要考查同角三角函数的基本关系,二倍角的正弦公式的应用,属于基础题.

练习册系列答案
相关题目
16.如图所示的程序框图中,输出的S的值是( )
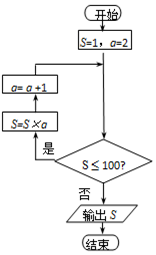

| A. | 80 | B. | 100 | C. | 120 | D. | 140 |
14.设f,g都是由A到A的映射,其对应法则如表(从上到下);
表1 映射f对应法则
表2 映射g的对应法则
则与f[g(1)]相同的是( )
表1 映射f对应法则
| 原像 | 1 | 2 | 3 | 4 |
| 像 | 3 | 4 | 2 | 1 |
| 原像 | 1 | 2 | 3 |
| 像 | 4 | 3 | 1 |
| A. | g[f(3)] | B. | g[f(2)] | C. | g[f(4)] | D. | g[f(1)] |