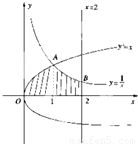
题目内容
 如图阴影部分是由曲线y=
如图阴影部分是由曲线y=| 1 |
| x |
| 2 |
| 3 |
| 2 |
| 3 |
分析:先求出y=
,y2=x的交点,然后利用积分的几何意义可得,S=
dx+
dx,结合积分基本定理可求
| 1 |
| x |
| ∫ | 1 0 |
| x |
| ∫ | 2 1 |
| 1 |
| x |
解答:解:由题意可得y=
,y2=x的交点为( 1,1)
由积分的几何意义可得,S=
dx+
dx
=
x
+lnx
=
+ln2.
故答案为:
+ln2.
| 1 |
| x |
由积分的几何意义可得,S=
| ∫ | 1 0 |
| x |
| ∫ | 2 1 |
| 1 |
| x |
=
| 2 |
| 3 |
| 3 |
| 2 |
| | | 1 0 |
| | | 2 1 |
| 2 |
| 3 |
故答案为:
| 2 |
| 3 |
点评:本题主要考查了积分基本定理及积分的几何意义的简单应用,属于基础试题.

练习册系列答案
相关题目
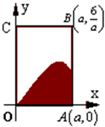 如图,矩形OABC内的阴影部分是由曲线f(x)=sinx(x∈(0,π))及直线x=a(a∈(0,π))与x轴围成,向矩形OABC内随机投掷一点,若落在阴影部分的概率为
如图,矩形OABC内的阴影部分是由曲线f(x)=sinx(x∈(0,π))及直线x=a(a∈(0,π))与x轴围成,向矩形OABC内随机投掷一点,若落在阴影部分的概率为 (2011•许昌一模)如图的阴影部分是由曲线y2=x与y=|x-2|的一部分围成,则它的面积为( )
(2011•许昌一模)如图的阴影部分是由曲线y2=x与y=|x-2|的一部分围成,则它的面积为( ) 如图,矩形OABC内的阴影部分是由曲线f(x)=sinx(x∈(0,π))及直线x=
如图,矩形OABC内的阴影部分是由曲线f(x)=sinx(x∈(0,π))及直线x= ,y2=x与直线x=2,y=0围成,则其面积为 .
,y2=x与直线x=2,y=0围成,则其面积为 .