题目内容
已知函数f(x)=x3+ax-2,(a∈R)
(l)若f(x)在区间(1,+∞)上是增函数,求实数a的取值范围;
(2)若g(x)=
,且f(x0)=3,求x0的值.
(3)若g(x)=
,且在R上是减函数,求实数a的取值范围.
(l)若f(x)在区间(1,+∞)上是增函数,求实数a的取值范围;
(2)若g(x)=
|
(3)若g(x)=
|
考点:导数在最大值、最小值问题中的应用
专题:导数的综合应用
分析:(1)根据导数的意义,f(x)在区间(1,+∞)上是增函数,则f′(x)=3x2+a≥0,在(1,+∞)上恒成立.从而解得a≥-3.
(2)首先化简g(x)的解析式,由f(x0)=3可得
或
.进而求出x0的值.
(3)首先化简g(x)的解析式,画出函数图象.依据图象即可得出当g(x)为减函数时实数a的取值范围为a≥1.
(2)首先化简g(x)的解析式,由f(x0)=3可得
|
|
(3)首先化简g(x)的解析式,画出函数图象.依据图象即可得出当g(x)为减函数时实数a的取值范围为a≥1.
解答:
解;(1)f′(x)=3x2+a,
∵f(x)在区间(1,+∞)上是增函数,
∴f′(x)=3x2+a≥0,在(1,+∞)上恒成立.
即a≥-3x2在(1,+∞)上恒成立.
∴a≥-3.
∴a的取值范围是[-3,+∞).
(2)g(x)=
,
即g(x)=
.
由f(x0)=3,
则
或
.
∴x0=-1或x0=
.
(3)g(x)=
.
即g(x)=
.
如右,图画出个g(x)的草图,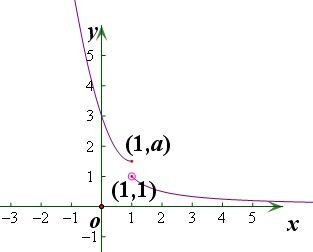
∵g(x)在R上是减函数,
∴
.
∴a≥1.
∵f(x)在区间(1,+∞)上是增函数,
∴f′(x)=3x2+a≥0,在(1,+∞)上恒成立.
即a≥-3x2在(1,+∞)上恒成立.
∴a≥-3.
∴a的取值范围是[-3,+∞).
(2)g(x)=
|
即g(x)=
|
由f(x0)=3,
则
|
|
∴x0=-1或x0=
| 1 |
| 3 |
(3)g(x)=
|
即g(x)=
|
如右,图画出个g(x)的草图,

∵g(x)在R上是减函数,
∴
|
∴a≥1.
点评:本题考查导数在最大最小值的应用,以及利用导数研究函数的单调性,数形结合思想在解题中的应用.属于难题.

练习册系列答案
相关题目
已知x,y满足约束条件
,则z=x+3y的最小值为( )
|
| A、1 | B、2 | C、3 | D、4 |
已知a、b都是实数,a≠0,f(x)=|x-1|+|x-2|.
(1)若f(x)>2,求实数x的取值范围;
(2)若|a+b|+|a-b|≥|a|f(x)对满足条件的所有a、b都成立,求实数x的取值范围.
(1)若f(x)>2,求实数x的取值范围;
(2)若|a+b|+|a-b|≥|a|f(x)对满足条件的所有a、b都成立,求实数x的取值范围.
二项式(
-
)n的展开式中第4项为常数项,则常数项为( )
| x |
| 1 | |||
|
| A、10 | B、-10 |
| C、20 | D、-20 |
