题目内容
设
=(cos(2x+
),sinx),
=(
,2sinx),f(x)=
•
.
(1)求f(x)的最小正周期;
(2)若∠A为锐角△ABC的一个内角,求f(A)的值域.
| a |
| π |
| 4 |
| b |
| ||
| 2 |
| a |
| b |
(1)求f(x)的最小正周期;
(2)若∠A为锐角△ABC的一个内角,求f(A)的值域.
考点:平面向量数量积的运算,三角函数的周期性及其求法
专题:平面向量及应用
分析:(1)利用三角恒等变换化简 f(x)=
•
=
cos(2x+
)+2sin2x 的解析式为1-
sin(2x+
),由此可得函数f(x)的最小正周期.
(2)根据0<∠A<
,利用正弦函数的定义域和值域求得f(A)的值域.
| a |
| b |
| ||
| 2 |
| π |
| 4 |
| ||
| 2 |
| π |
| 4 |
(2)根据0<∠A<
| π |
| 2 |
解答:
解:(1)由题意可得 f(x)=
•
=
cos(2x+
)+2sin2x
=
(cos2x•
-sin2x•
)+1-cos2x=1-
(sin2x+cos2x)
=1-
sin(2x+
),
故函数f(x)的最小正周期为
=π.
(2)∵0<∠A<
,
∴
<2∠A+
<
,
∴-
sin(2A+
)≤1,
∴1-
≤f(A)<1+
=
,
即f(A)的值域为[1-
,
).
| a |
| b |
| ||
| 2 |
| π |
| 4 |
=
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| 1 |
| 2 |
=1-
| ||
| 2 |
| π |
| 4 |
故函数f(x)的最小正周期为
| 2π |
| 2 |
(2)∵0<∠A<
| π |
| 2 |
∴
| π |
| 4 |
| π |
| 4 |
| 5π |
| 4 |
∴-
| ||
| 2 |
| π |
| 4 |
∴1-
| ||
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
即f(A)的值域为[1-
| ||
| 2 |
| 3 |
| 2 |
点评:本题主要考查两个向量的数量积的运算,三角恒等变换,正弦函数的周期性、定义域和值域,属于中档题.

练习册系列答案
相关题目
在5×5的棋盘中,放入3颗黑子和2颗白子,它们均不在同一行且不在同一列,则不同的排列方法种数为( )
| A、150 | B、200 |
| C、600 | D、1200 |
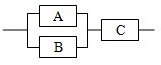 某个部件由三个元件如图方式连接而成,元件A或元件B正常工作,且元件C正常工作,则部件正常工作.若3个元件的次品率均为
某个部件由三个元件如图方式连接而成,元件A或元件B正常工作,且元件C正常工作,则部件正常工作.若3个元件的次品率均为